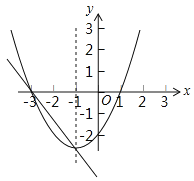题目内容
【题目】如图,抛物线y=![]() x2+bx+c与x轴交于点A(﹣1,0),B(4,0)与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线1,交抛物线与点Q.
x2+bx+c与x轴交于点A(﹣1,0),B(4,0)与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线1,交抛物线与点Q.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,直线1交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;
(3)在点P运动的过程中,坐标平面内是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
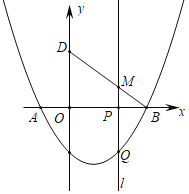
【答案】(1) ![]() ;(2) 当m=2时,四边形CQMD为平行四边形;(3) Q1(8,18)、Q2(﹣1,0)、Q3(3,﹣2)
;(2) 当m=2时,四边形CQMD为平行四边形;(3) Q1(8,18)、Q2(﹣1,0)、Q3(3,﹣2)
【解析】
(1)直接将A(-1,0),B(4,0)代入抛物线y=![]() x2+bx+c方程即可;
x2+bx+c方程即可;
(2)由(1)中的解析式得出点C的坐标C(0,-2),从而得出点D(0,2),求出直线BD:y=![]() x+2,设点M(m,
x+2,设点M(m,![]() m+2),Q(m,
m+2),Q(m,![]() m2
m2![]() m2),可得MQ=
m2),可得MQ=![]() m2+m+4,根据平行四边形的性质可得QM=CD=4,即
m2+m+4,根据平行四边形的性质可得QM=CD=4,即![]() m2+m+4=4可解得m=2;
m2+m+4=4可解得m=2;
(3)由Q是以BD为直角边的直角三角形,所以分两种情况讨论,①当∠BDQ=90°时,则BD2+DQ2=BQ2,列出方程可以求出Q1(8,18),Q2(-1,0),②当∠DBQ=90°时,则BD2+BQ2=DQ2,列出方程可以求出Q3(3,-2).
(1)由题意知,
∵点A(﹣1,0),B(4,0)在抛物线y=![]() x2+bx+c上,
x2+bx+c上,
∴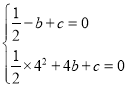 解得:
解得: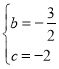
∴所求抛物线的解析式为 ![]()
(2)由(1)知抛物线的解析式为![]() ,令x=0,得y=﹣2
,令x=0,得y=﹣2
∴点C的坐标为C(0,﹣2)
∵点D与点C关于x轴对称
∴点D的坐标为D(0,2)
设直线BD的解析式为:y=kx+2且B(4,0)
∴0=4k+2,解得:![]()
∴直线BD的解析式为:![]()
∵点P的坐标为(m,0
∴可设点M![]() ,Q
,Q![]()
∴MQ=![]()
∵四边形CQMD是平行四边形
∴QM=CD=4,即![]() =4
=4
解得:m1=2,m2=0(舍去)
∴当m=2时,四边形CQMD为平行四边形
(3)由题意,可设点Q![]() 且B(4,0)、D(0,2)
且B(4,0)、D(0,2)
∴BQ2=![]()
DQ2=![]()
BD2=20
①当∠BDQ=90°时,则BD2+DQ2=BQ2,
∴![]()
解得:m1=8,m2=﹣1,此时Q1(8,18),Q2(﹣1,0)
②当∠DBQ=90°时,则BD2+BQ2=DQ2,
∴![]()
解得:m3=3,m4=4,(舍去)此时Q3(3,﹣2)
∴满足条件的点Q的坐标有三个,分别为:Q1(8,18)、Q2(﹣1,0)、Q3(3,﹣2).

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案