题目内容
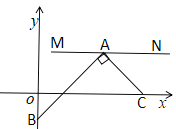
【题目】如图1，在平面直角坐标系xOy中，已知△ABC，∠ABC=90°，顶点A在第一象限，B，C在x轴的正半轴上（C在B的右侧），BC=2，AB=2
，△ADC与△ABC关于AC所在的直线对称．
（1）当OB=2时，求点D的坐标；
（2）若点A和点D在同一个反比例函数的图象上，求OB的长；
（3）如图2，将第（2）题中的四边形ABCD向右平移，记平移后的四边形为A1B1C1D1，过点D1的反比例函数y=
（k≠0）的图象与BA的延长线交于点P．问：在平移过程中，是否存在这样的k，使得以点P，A1，D为顶点的三角形是直角三角形？若存在，请直接写出所有符合题意的k的值；若不存在，请说明理由．
【答案】（1）点D坐标为（5，
）；（2）OB=3；（3）k=12．
【解析】（1）如图1中，作DE⊥x轴于E，解直角三角形清楚DE，CE即可解决问题；
（2）设OB=a，则点A的坐标（a，2），由题意CE=1．DE=，可得D（3+a，），点A、D在同一反比例函数图象上，可得2a=（3+a），求出a的值即可；
（3）分两种情形：①如图2中，当∠PA1D=90°时．②如图3中，当∠PDA1=90°时．分别构建方程解决问题即可；
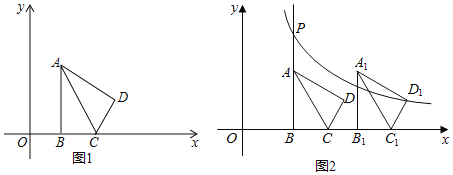
（1）如图1中，作DE⊥x轴于E．
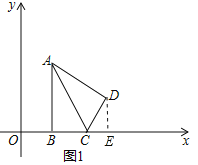
∵∠ABC=90°，
∴tan∠ACB=
，
∴∠ACB=60°，
根据对称性可知：DC=BC=2，∠ACD=∠ACB=60°，
∴∠DCE=60°，
∴∠CDE=90°-60°=30°，
∴CE=1，DE=，
∴OE=OB+BC+CE=5，
∴点D坐标为（5，）．
（2）设OB=a，则点A的坐标（a，2），
由题意CE=1．DE=，可得D（3+a，），
∵点A、D在同一反比例函数图象上，
∴2a=（3+a），
∴a=3，
∴OB=3．
（3）存在．理由如下：
①如图2中，当∠PA1D=90°时．
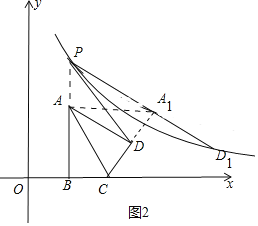
∵AD∥PA1，
∴∠ADA1=180°-∠PA1D=90°，
在Rt△ADA1中，∵∠DAA1=30°，AD=2，
∴AA1=
=4，
在Rt△APA1中，∵∠APA1=60°，
∴PA=
，
∴PB=
，
设P（m，），则D1（m+7，），
∵P、A1在同一反比例函数图象上，
∴m=（m+7），
解得m=3，
∴P（3，），
∴k=10．
②如图3中，当∠PDA1=90°时．
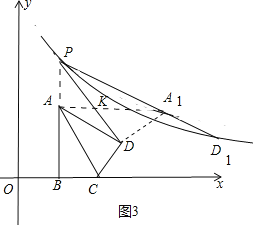
∵∠PAK=∠KDA1=90°，∠AKP=∠DKA1，
∴△AKP∽△DKA1，
∴
．
∴
，
∵∠AKD=∠PKA1，
∴△KAD∽△KPA1，
∴∠KPA1=∠KAD=30°，∠ADK=∠KA1P=30°，
∴∠APD=∠ADP=30°，
∴AP=AD=2，AA1=6，
设P（m，4），则D1（m+9，），
∵P、A1在同一反比例函数图象上，
∴4m=（m+9），
解得m=3，
∴P（3，4），
∴k=12．
