题目内容
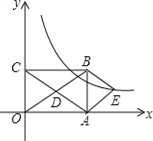
【题目】如图,A,B是反比例函数y=![]() 图象上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=
图象上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=![]() OC,S四边形ABCD=9,则k值为( )
OC,S四边形ABCD=9,则k值为( )
A.8B.10C.12D.16.
【答案】B
【解析】
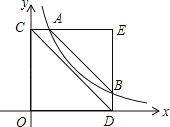
分别延长CA、DB,它们相交于E,如图,设AC=t,则BD=t,OC=5t,根据反比例函数图象上点的坐标特征得到k=ODt=t5t,则OD=5t,所以B点坐标为(5t,t),于是AE=CE﹣CA=4t,BE=DE﹣BD=4t,再利用S四边形ABCD=S△ECD﹣S△EAB得到![]() 5t5t﹣
5t5t﹣![]() 4t4t=9,解得t2=2,然后根据k=t5t进行计算.
4t4t=9,解得t2=2,然后根据k=t5t进行计算.
解:分别延长CA、DB,它们相交于E,如图,
设AC=t,则BD=t,OC=5t,
∵A,B是反比例函数y=![]() 图象上两点,
图象上两点,
∴k=ODt=t5t,
∴OD=5t,
∴B点坐标为(5t,t),
∴AE=CE﹣CA=4t,BE=DE﹣BD=4t,
∵S四边形ABCD=S△ECD﹣S△EAB,
∴![]() 5t5t﹣
5t5t﹣![]() 4t4t=9,
4t4t=9,
∴t2=2,
∴k=t5t=5t2=5×2=10.
故选:B.

练习册系列答案
相关题目