Question

【题目】已知AB是⊙O的直径，DA为⊙O的切线，切点为A，过⊙O上的点C作CD∥AB交AD于点D，连接BC、AC．

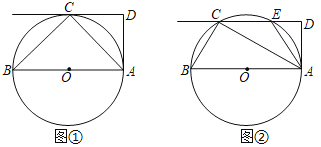
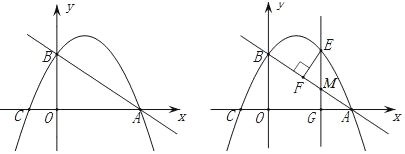
（1）如图①，若DC为⊙O的切线，切点为C，求∠ACD和∠DAC的大小．

（2）如图②，当CD为⊙O的割线且与⊙O交于点E时，连接AE，若∠EAD＝30°，求∠ACD和∠DAC的大小．

Answer 1

【答案】（1）∠ACD＝∠DAC＝45°；（2）∠ACD＝30°，∠DAC＝60°．

【解析】

（1）先根据题意确定三角形ADC是等腰直角三角形，进而求出∠ACD和∠DAC的大小；

（2）根据AB是圆O的直径，DA为圆O的切线，切点为A，可得DA⊥AB，根据∠EAD=30°，可得∠BAE=60°，根据圆内接四边形对角互补可得∠BCE=120°，根据AB是圆O的直径，可得∠BCA=90°，进而求得∠ACD和∠DAC的大小．

（1）∵AB是⊙O的直径，DA为⊙O的切线，切点为A，

∴DA⊥AB，

∴∠DAB＝90°，

∵DC为⊙O的切线，切点为C，

∴DC＝DA，

∵CD∥AB，

∴∠D+∠DAB＝180°，

∴∠D＝90°，

∴∠ACD＝∠DAC＝45°；

（2）∵AB是⊙O的直径，DA为⊙O的切线，切点为A，

∴DA⊥AB，

∴∠DAB＝90°，

∠DEA＝∠EAB，

∴∠ADC＝90°，

∵∠EAD＝30°，

∴∠DEA＝60°，

∴∠EAB＝60°，

∴∠BCE＝120°，

∵AB是⊙O的直径，

∴∠BCA＝90°，

∴∠ACD＝30°，

∴∠DAC＝60°．