Question

【题目】如图，已知：抛物线y＝a（x+1）（x﹣3）交x轴于A、C两点，交y轴于B．且OB＝2CO．

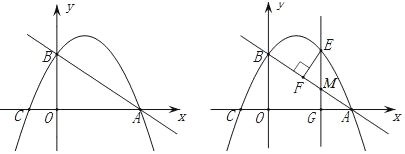
（1）求点A、B、C的坐标及二次函数解析式；

（2）在直线AB上方的抛物线上有动点E，作EG⊥x轴交x轴于点G，交AB于点M，作EF⊥AB于点F．若点M的横坐标为m，求线段EF的最大值．

（3）抛物线对称轴上是否存在点P使得△ABP为直角三角形，若存在请直接写出点P的坐标；若不存在请说明理由．

Answer 1

【答案】（1）y= ;（2）；（3）点P的坐标为（1，﹣3）或（1，）或（1，1+）或（1，1﹣），理由见解析

【解析】

（1）利用待定系数法求出、、的坐标即可解决问题；

（2）易用表示线段的长度，再求得和的长度关系，根据等角三角函数或三角形相似即可解题；

（3）为直角三角形时，分别以三个顶点为直角顶点讨论：根据三角形相似和勾股定理列方程解决问题.

（1）对于抛物线y＝a（x+1）（x﹣3），令y＝0，得到a（x+1）（x﹣3）＝0，解得x＝﹣1或3，

∴C（﹣1，0），A（3，0），

∴OC＝1，

∵OB＝2OC＝2，

∴B（0，2），

把B（0，2）代入y＝a（x+1）（x﹣3）中得：2＝﹣3a，，

∴二次函数解析式为；

（2）设直线AB的解析式为：y＝kx+b，

把A（3，0），B（0，2）代入得：，解得：，

∴直线AB的解析式为：，

由题意可设，，

则；

∵在Rt△AOB中，根据勾股定理，得，

∵∠EMF+∠FEM＝∠AMG+∠BAO＝90°，

∵∠AMG＝∠EMF，

∴∠FEM＝∠BAO，

，

∴，

∴，

∴当时，EF有最大值是；

（3）∵A（3，0），B（0，2），

∴OA＝3，OB＝2，

由对称得：抛物线的对称轴是：x＝1，

∴AE＝3﹣1＝2，

设抛物线的对称轴与x轴相交于点E，当△ABP为直角三角形时，存在以下三种情况：

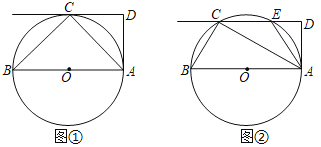
①如图1，当∠BAP＝90°时，点P在AB的下方，

∵∠PAE+∠BAO＝∠BAO+∠ABO＝90°，

∴∠PAE＝∠ABO，

∵∠AOB＝∠AEP，

∴△ABO∽△PAE，

∴，即，

∴PE＝3，

∴P（1，﹣3）；

②如图2，当∠PBA＝90°时，点P在AB的上方，过P作PF⊥y轴于F，

同理得：△PFB∽△BOA，

∴，即，

∴，

∴，

∴；

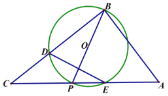
③如图3，以AB为直径作圆与对称轴交于P1、P2，则∠AP1B＝∠AP2B＝90°，

设P1（1，y），

∵AB2＝22+32＝13，

由勾股定理得：AB2＝P1B2+P1A2，

∴12+（y﹣2）2+（3﹣1）2+y2＝13，

解得：，

∴或，

综上所述，点P的坐标为（1，﹣3）或（1，）或（1，1+）或（1，1﹣）．