Question

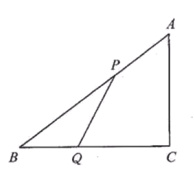
【题目】如图，在直角三角形ABC中，直角边，，设P、Q分别为AB，BC上的动点，点P自点A沿AB方向向点B作匀速移动且速度为每秒2cm，同时点Q自点B沿BC方向向点C作匀速移动且速度为每秒1cm，当P点到达B点时，Q点就停止移动.设P，Q移动的时间t秒.

（1）写出的面积S（）与时间t（s）之间的函数表达式，并写出t的取值范围.

（2）当t为何值时，为等腰三角形？

Answer 1

【答案】（1）；（2）当t或或时，为等腰三角形.

【解析】

（1）过点P作PH⊥BC，垂足为H，从而得到△BPH∽△ABC，根据相似比例求出PH的长，然后表示出三角形PBQ的面积即可；

（2）需要分BP=BQ，BQ=PQ和BP=PQ三种情况讨论三角形PBQ为等腰三角形，即最后分别求值即可.

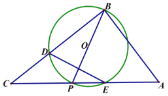
（1）如图1，过点P作PH⊥BC，垂足为H，

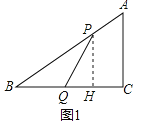
∵Rt△ABC中直角边AC=6，BC=8

∴由勾股定理可得AB=10，

∴BP=10-2t，BQ=t.

∵AC⊥C B

∴△BPH∽△ABC，

∴ 即，解得;

∴

（2）①当BP=BQ时，10-2t=t，解得t= 秒；

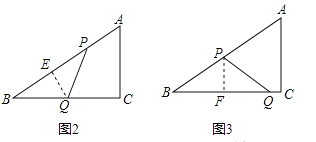
②如图2，当BQ=PQ时，作QE⊥BD，垂足为E，

∵BQ=PO，QE⊥BD，

∴

∵∠B=∠B, ∠ACB=∠QEB,

∴△BQE∽△BAC

∴，即，即得：t= 秒；

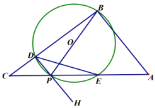
③如图3，当BP=PQ时，作PF⊥BC，垂足为F

∵BP=PQ，PF⊥BC，

∴

∵

∴△BPF∽△BAC，

∴，即：，解得：t=秒

综上：当或或时，为等腰三角形.