题目内容
(11·大连)如图2,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF等于

A. | B.1 | C. | D.2 |

C
分析:根据矩形的性质得到AD=BC=5,∠D=∠B=∠C=90°,根据三角形的角平分线的性质得到DF=EF,由勾股定理求出AE、BE,证△ABE∽△ECF,得出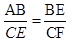 ,代入求出即可.
,代入求出即可.
解答:解:∵四边形ABCD是矩形,
∴AD=BC=5,∠D=∠B=∠C=90°,
∵AF平分∠DAE,EF⊥AE,
∴DF=EF,
由勾股定理得:AE2=AF2-EF2,AD2=AF2-DF2,
∴AE=AD=5,
在△ABE中由勾股定理得:BE=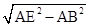 =3,
=3,
∴EC=5-3=2,
∵∠BAE+∠AEB=90°,∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF,
∴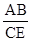 =
=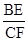 ,
,
∴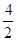 =
=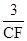 ,
,
∴CF=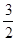 .
.
故选C.
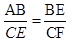 ,代入求出即可.
,代入求出即可.解答:解:∵四边形ABCD是矩形,
∴AD=BC=5,∠D=∠B=∠C=90°,
∵AF平分∠DAE,EF⊥AE,
∴DF=EF,
由勾股定理得:AE2=AF2-EF2,AD2=AF2-DF2,
∴AE=AD=5,
在△ABE中由勾股定理得:BE=
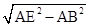 =3,
=3,∴EC=5-3=2,
∵∠BAE+∠AEB=90°,∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF,
∴
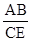 =
=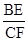 ,
,∴
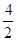 =
=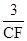 ,
,∴CF=
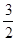 .
.故选C.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目









