题目内容
【题目】（1）操作：如图，在已知内角度数的三个三角形中，请用直尺从某一顶点画一条线段，把原三角形分割成两个等腰三角形，并在图中标注相应的角的度数
（2）拓展，△ABC中，AB=AC，∠A=45°，请把△ABC分割成三个等腰三角形，并在图中标注相应的角的度数.
（3）思考在如图所示的三角形中∠A=30°.点P和点Q分别是边AC和BC上的两个动点.分别连接BP和PQ把△ABC分割成三个三角形.△ABP，△BPQ，△PQC若分割成的这三个三角形都是等腰三角形，求∠C的度数所有可能值直接写出答案即可.
【答案】（1）见解析；（2）见解析；（3）∠C所有可能的值为10°、20°、25°，35°、40°、50°、80°、100°.
【解析】
（1）在图1、图2、图3中，分别作AB、AB、BC的垂直平分线，根据垂直平分线的性质及外角的性质求出各角度数即可；（2）分别作AB、BC的垂直平分线，交于点O，连接OA、OB、OC可得三角形OAB、OAC、OBC为等腰三角形，根据等腰三角形的性质及外角性质求出各角度数即可；（3）分PB=PA、AB=AP、BA=BP时，PB=PQ、BP=BQ、QB=QP，PQ=QC、PC=QC、PQ=PC等10种情况，根据等腰三角形的性质分别求出∠C的度数即可.
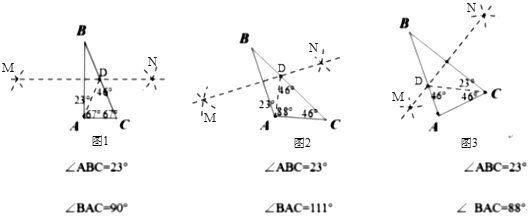
（1）在图1、图2、图3中，分别作AB、AB、BC的垂直平分线，
如图1，∵∠ABC=23°，∠BAC=90°，
∴∠C=90°-23°=67°，
∵MN垂直平分AB，
∴BD=AD，
∴△ABD是等腰三角形，
∴∠BAD=∠ABC=23°，
∴∠ADC=2∠ABC=46°，
∵∠BAC=90°，
∴∠DAC=∠BAC-∠BAD=67°，
∴∠DAC=∠C，
∴△DAC是等腰三角形，
同理：图2中，∠ADC=46°，∠DAC=88°，∠C=46°，△ABD和△ACD是等腰三角形，
图3中，∠BCD=23°，∠ADC=46°，∠ACD=46°，△BCD和△ACD是等腰三角形.
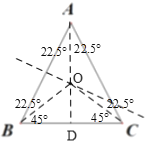
（2）作AB、BC的垂直平分线，交于点O，连接OA、OB、OC，
∵点O是三角形垂直平分线的交点，
∴OA=OB=OC，
∴△OAB、△OAC、△OBC是等腰三角形，
∵AB=AC，∠BAC=45°，
∴∠ABC=∠ACB=67.5°，
∴AD是BC的垂直平分线，
∴∠BAD=∠CAD=22.5°，
∴∠OBA=∠OAB=22.5°，∠OCA=∠OAC=22.5°，
∴∠OBC=∠OCB=45°.
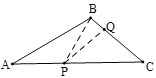
（3）①如图，当PB=PA，PB=PQ，PQ=CQ时，
∵∠A=30°，PB=PQ，
∴∠ABP=∠A=30°，
∴∠APB=120°，
∵PB=PQ，PQ=CQ，
∴∠PQB=∠PBQ，∠C=∠CPQ，
∴∠PBQ=2∠C，
∴∠APB=∠PBQ+∠C=3∠C=120°，
解得：∠C=40°.
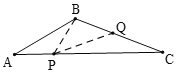
②如图，当PB=PA，PB=BQ，PQ=CQ时，
∴∠PQB=2∠C，∠PQB=∠BPQ，
∴∠PBQ=180°-2∠PQB=180°-4∠C，
∴180°-4∠C+∠C=120°，
解得：∠C=20°，
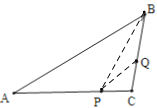
③如图，当PA=PB，BQ=PQ，CQ=CP时，
∵∠PQC=2∠PBQ，∠PQC=
（180°-∠C），
∴∠PBQ=
（180°-∠C），
∴（180°-∠C）+∠C=120°，
解得：∠C=100°.
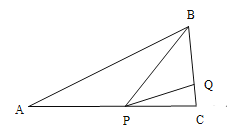
④如图，当PA=PB，BQ=PQ，PQ=CP时，
∵∠PQC=∠C=2∠PBQ,
又∵∠C+∠PBQ=120°，
∴∠C=80°；
⑤如图，当AB=AP，BP=BQ，PQ=QC时，
∵∠A=30°，
∴∠APB=（180°-30°）=75°，
∵BP=BQ，PQ=CQ，
∴∠BPQ=∠BQP，∠QPC=∠QCP，
∴∠BQP=2∠C，
∴∠PBQ=180°-4∠C，
∴∠C+180°-4∠C=75°，
解得：∠C=35°.
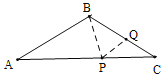
⑥如图，当AB=AP，BQ=PQ，PC=QC时，
∴∠PQC=2∠PBC，∠PQC=（180°-∠C），
∴∠PBC=（180°-∠C），
∴（180°-∠C）+∠C=75°，
解得：∠C=40°.
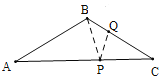
⑦如图，当AB=AP，BQ=PQ，PC=QP时，
∵∠C=∠PQC=2∠PBC，∠C+∠PQC=75°，
∴∠C=50°；
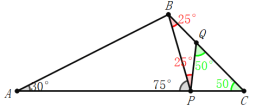
⑧当AB=AP，BP=PQ，PQ=CQ时，
∵AB=BP，∠A=30°，
∴∠ABP=∠APB=75°，
又∵∠PBQ=∠PQB=2∠C，
且有∠PBQ+∠C=180°-30°-75°=75°，
∴3∠C=75°，
∴∠C=25°；
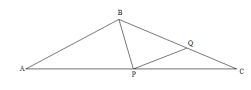
⑨当AB=BP，BP=PQ，PQ=CQ时，
∵AB=BP，
∴∠BPA=∠A=30°，
∵∠PBQ=∠PQB=2∠C，
∴2∠C+∠C=30°，
解得：∠C=10°.
⑩当AB=BP，BQ=PQ，PQ=CQ时，
∴∠PQC=∠C=2∠PBQ，
∴∠C+∠C=30°，
解得：∠C=20°.
综上所述：∠C所有可能的值为10°、20°、25°，35°、40°、50°、80°、100°.
