题目内容
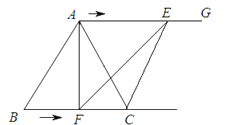
【题目】如图,在等边三角形ABC中,BC=6![]() ,射线AG∥BC,点E从点A出发沿射线AG以
,射线AG∥BC,点E从点A出发沿射线AG以![]() 的速度运动,同时点F从点B出发沿射线BC以
的速度运动,同时点F从点B出发沿射线BC以![]() 的速度运动,设运动时间为
的速度运动,设运动时间为![]()

(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF
(2)填空:
①当![]() 为 s时,四边形ACFE是菱形;
为 s时,四边形ACFE是菱形;
②当![]() 为 s时,以A,F,C,E为顶点的四边形是直角梯形.
为 s时,以A,F,C,E为顶点的四边形是直角梯形.
【答案】(1)见解析;(2)①6; ②![]()
【解析】
(1)∵AG∥BC,
∴∠EAD=∠ACB.
∵D是AC边的中点,
∴AD=CD.
又∵∠ADE=∠CDF ,
∴△ADE≌△CDF(ASA).
(2)①∵当四边形ACFE是菱形时,
∴AE=AC=CF=EF.
由题意可知:AE=![]() ,CF=
,CF=![]() ,
,
∴![]() ,即
,即![]() .
.
②若EF⊥AG,四边形ACFE是直角梯形,
过C作CM⊥AG于点M,
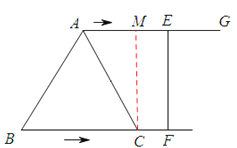
∵AM=3,AE=![]() ,ME=CF=
,ME=CF=![]() ,
,
∴AE-ME=AM,,即![]() ,
,
此时,G与F重合,不符合题意,舍去.
若AF⊥BV,四边形若四边形AFCE是直角梯形,
∵△ABC是等边三角形,F是BC中点,
∴![]() ,解得
,解得![]() .
.
经检验,符合题意.

练习册系列答案
相关题目