题目内容
【题目】(12分)平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-4,0),B(2,0),C(3,3),反比例函数y=![]() 的图象经过点C.
的图象经过点C.
(1)求此反比例函数的解析式;
(2)将平行四边形ABCD沿x轴翻折得到平行四边形ABC′D′,请说明点D′在双曲线上;
(3)连接AC,CD′,求△ACD′的面积.

【答案】(1)![]() ;(2)点D′在双曲线上;(3)12.
;(2)点D′在双曲线上;(3)12.
【解析】试题分析:(1)根据反比例函数图象点的坐标特征把C点坐标代入y=![]() ,求出k的值即可确定反比例函数解析式;
,求出k的值即可确定反比例函数解析式;
(2)先计算出AB=10,再根据平行四边形的性质得CD=10,则可确定D点坐标为(-5,3),然后根据关于x轴对称的点的坐标特征得D′的坐标为(-5,-3)再根据反比例函数图象点的坐标特征判断点D′在双曲线上;
(3)由于点C坐标为(5,3),D′的坐标为(-5,-3),则点C和点D′关于原点中心对称,根据中心对称的性质得点D′、O、C共线,且OC=OD′,然后利用S△AD′C=S△AD′O+S△AOC=2S△AOC进行计算.
试题解析:(1)∵C(5,3)在反比例函数y=![]() 的图象上,
的图象上,
∴![]() =3,
=3,
∴k=15,
∴反比例函数解析式为y=![]() ;
;
(2)∵A(-6,0),B(4,0),
∴AB=10,
∵四边形ABCD为平行四边形,
∴CD=10,
而C点坐标为(5,3),
∴D点坐标为(-5,3),
∵平行四边形ABCD和平行四边形AD′C′B关于x轴对称,
∴D′的坐标为(-5,-3),
∵-5×(-3)=15,
∴点D′在双曲线y=![]() 上;
上;
(3)如图,
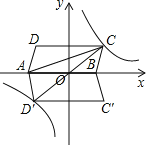
∵点C坐标为(5,3),D′的坐标为(-5,-3),
∴点C和点D′关于原点中心对称,
∴点D′、O、C共线,且OC=OD′,
∴S△AD′C=S△AD′O+S△AOC=2S△AOC=2×![]() ×6×3=18.
×6×3=18.