题目内容
【题目】如图,Rt△ABC中,∠CAB=90°,在斜边CB上取点M,N(不包含C、B两点),且tanB=tanC=tan∠MAN=1,设MN=x,BM=n,CN=m,则以下结论能成立的是( )

A. m=n B. x=m+n C. x>m+n D. x2=m2+n2
【答案】D
【解析】
将△ABM绕点A顺时针旋转90°至△ACN′,连接NN′;证明△AMN≌△ANN′,则有MN=NN′;在Rt△NN'C′中,根据勾股定理可得结论.
∵tanB=tanC=tan∠MAN=1,
∴∠B=∠C=∠MAN=45°,
∵∠CAB=90°,
∴AC=AB,
将△BAM绕点A顺时针旋转90°至△ACN′,点B与点C重合,点M落在N′处,连接NN′,
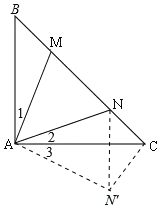
则有AN′=AM,CN′=BM,∠1=∠3,
∵∠MCN=45°,
∴∠1+∠2=45°,
∴∠2+∠3=45°,
∴∠NAN′=∠MAN.
在△MAN与△NAN′中,
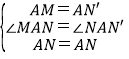 ,
,
∴△MAN≌△NCN′(SAS),
∴MN=NN′,
由旋转性质可知,∠ACN′=∠B=45°,
∴∠NCN′=∠ACN′+∠ACB=90°,
∴NN'2=NC2+N'C2,
即x2=n2+m2,
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目