题目内容
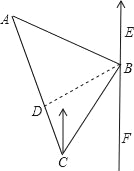
【题目】如图,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB.

【答案】15![]()
【解析】
此题可先由速度和时间求出BC的距离,再由各方向角得出∠A的角度,过B作BD⊥AC于D,求出∠DBC=30°,求出DC,由勾股定理求出BD,求出AD、BD的长,由勾股定理求出AB即可.
由示意图可知:∠ACB=60°,
由平行线的性质可知∠ABC=180°﹣30°﹣75°=75°,
∴∠A=180°﹣∠C﹣∠B=45°,BC=60×![]() =30(海里),
=30(海里),
过B作BD⊥AC于D,
则∠BDC=90°,∠DBC=30°,
∴DC=![]() BC=15海里,
BC=15海里,
由勾股定理得:BD=15![]() 海里,
海里,
∵∠A=45°,∠ADB=90°,
∴∠ABD=∠A=45°,
∴AD=BD=15![]() 海里,
海里,
由勾股定理得:AB=![]() (海里),
(海里),
答:此时货轮距灯塔A的距离AB为![]() 海里.
海里.

练习册系列答案
相关题目