��Ŀ����
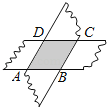
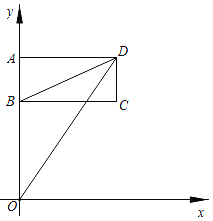
����Ŀ����ͼ��������ABCD��ƽ��ֱ������ϵ�У���֪��A��0��a����B��0��6����C��b��6����������a=![]() +8��
+8��
��1����ֱ��д��A��C��D����������꣬A�� ����C�� ����D�� ����
��2�������߶�BD��OD������������BOD�������
��3����������ABCD��ÿ��1����λ�������������˶������˶���ʱ��Ϊt�룬���Ƿ����ijһʱ�̣�������BOD������볤����ABCD�������ȣ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��A��0��8����C��4��6����D��4��8������2��12����3�����ڣ�2��10��
��������
��1�����ö��θ�ʽ���������a��b��ֵ���ɽ�����⣻
��2�����������ε������ʽ���㼴�ɣ�
��3�����������ηֱ���㼴�ɣ�
�⣺��1���� a=![]() +8,
+8,
�֡�![]()
![]() ��
��
��b=4��a=8��
��A��0��8����C��4��6����D��4��8����
�ʴ�Ϊ��0��8������4��6������4��8����
(2)�����⣺![]() .
.
��3�����ڣ�
���ɣ���������ABCD��x����Ϸ�ʱ.BO=6-t,��![]() ��4����6-t��=2��4,
��4����6-t��=2��4,
���t=2,
��������ABCD��x����·�ʱ.BO=t-6,
��![]() ��4��t-6��=2��4,
��4��t-6��=2��4,
���t=10,
���˶���ʱ��2��10��ʱ��������BOD������볤����ABCD�������ȣ�

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�����Ŀ��ij�����ƻ�����A��B���ֲ�Ʒ��10�����������ɱ����������±���
A�ֲ�Ʒ | B�ֲ�Ʒ | |
�ɱ�����Ԫ/���� | 2 | 5 |
������Ԫ/���� | 1 | 3 |
��1���������ƻ�����14��Ԫ����A��B���ֲ�ƷӦ�ֱ��������ټ���
��2���������ƻ�Ͷ���ʽ���44��Ԫ���һ�������14��Ԫ���ʹ������ļ�������������
��3���ڣ�2���������£������������������������������