题目内容
如图,已知:AC⊥AB,BD⊥AB,且AC=BE,AE=BD,求证:△CDE是等腰直角三角形;
证明:∵AC⊥AB,BD⊥AB ∴∠CAE=∠DBE=90°
∵AC= BE,AE=BD ∴△ACE≌△BED
∴CE=DE且∠ACE=∠BED
∵∠ACE+∠AEC=90° ∴∠AEC+∠BED=90°
∴∠CED=90° ∴△CED为等腰直角三角形
利用上题的解题思路解答下列问题:
在Rt△ABC中,∠C=90°,D,E分别为CB,CA延长线上的点,BE与AD的交点为P.
【小题1】若BD=AC,AE=CD,在下图中画出符合题意的图形,求出∠APE的度数;
【小题2】若AC=BD,CD=AE,则∠APE=__________°
p;【答案】
【小题1】过E作EQ^AE,且使EQ=AC……………1分
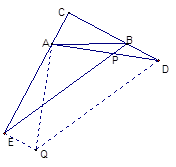
∴∠AEQ=90°,∵∠C=90°
∴∠AEQ=∠C
∵EQ=AC AE=CD
∴△AEQ≌△DCA……………4分
∴AQ=AD ∠EAQ=∠CDA
∵∠CAD+∠CDA=90°
∴∠EAQ+∠CAD=90°
∴∠QAD=90°……………5分
∴∠ADQ=45°……………6分
∵∠QAE=90° ∠C=90°
∴∠QAE+∠C=180°
∴EQ∥BC ∵AC=BD
∴EQ=BD
∴ 四边形EQDB是平形四边形……………7分
∴BE∥DQ ∴∠APE=∠ADQ=45°……………8分
【小题2】30°解析:
略
【小题1】过E作EQ^AE,且使EQ=AC……………1分

∴∠AEQ=90°,∵∠C=90°
∴∠AEQ=∠C
∵EQ=AC AE=CD
∴△AEQ≌△DCA……………4分
∴AQ=AD ∠EAQ=∠CDA
∵∠CAD+∠CDA=90°
∴∠EAQ+∠CAD=90°
∴∠QAD=90°……………5分
∴∠ADQ=45°……………6分
∵∠QAE=90° ∠C=90°
∴∠QAE+∠C=180°
∴EQ∥BC ∵AC=BD
∴EQ=BD
∴ 四边形EQDB是平形四边形……………7分
∴BE∥DQ ∴∠APE=∠ADQ=45°……………8分
【小题2】30°解析:
略

练习册系列答案
相关题目
 如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,则∠BFD的度数是( )
如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,则∠BFD的度数是( )| A、60° | B、90° | C、45° | D、120° |
 如图,已知AB=AC,D、E分别为AB、AC的中点,G、H分别为AD、AE的中点,则图中的全等三角形共有( )
如图,已知AB=AC,D、E分别为AB、AC的中点,G、H分别为AD、AE的中点,则图中的全等三角形共有( ) 如图,已知BD⊥AC于点D,CE⊥AB于点E,BD=EC,则△ABD≌△ACE,其依据是( )
如图,已知BD⊥AC于点D,CE⊥AB于点E,BD=EC,则△ABD≌△ACE,其依据是( ) 如图,已知AB=AC,AD=AE,∠BAE=30°,则∠CED=
如图,已知AB=AC,AD=AE,∠BAE=30°,则∠CED= 如图,已知AB=AC,DB=DC,试说明∠ABD=∠ACD.
如图,已知AB=AC,DB=DC,试说明∠ABD=∠ACD.