题目内容
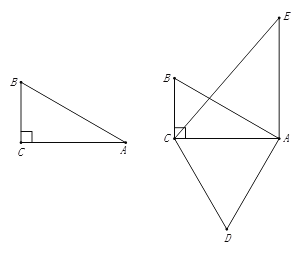
【题目】如图1,直角三角形ABC中,∠C=90°,CB=1,∠BAC=30°.
(1)求AB、AC的长;
(2)如图2,将AB绕点A顺时针旋转60°得到线段AE,将AC绕点A逆时针旋转60°得到线段AD.
①连接CE,BD.求证:BD=EC;
②连接DE交AB于F,请你作出符合题意的图形并求出DE的长
【答案】(1)AB=2,AC=![]() ;(2)①证明见解析;②图形见解析,DE=
;(2)①证明见解析;②图形见解析,DE=![]() .
.
【解析】
(1)根据含30°角的直角三角形的性质求出AB,再利用勾股定理求出AC即可;
(2)①根据旋转的性质得到AB=AE,AC=AD,∠BAE=∠CAD=60°,再利用SAS证明△AEC≌△ABD,从而可得到结论;
②过点D作DM⊥AE,交EA的延长线于点M,可证明∠CAE=90°,从而求得∠DAM=30°,在Rt△ADM中利用含30°角的直角三角形的性质及勾股定理可求出DM、AM,最后在Rt△DME中利用勾股定理求出DE即可.
解:(1)∵∠C=90°,∠BAC=30°,且BC=1,
∴AB=2BC=2,
∴在Rt△ABC中,AC=![]() ;
;
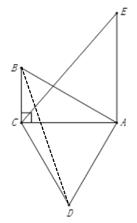
(2)①证明:如图所示:
由旋转可得,AB=AE=2,AC=AD=![]() ,∠BAE=∠CAD=60°,
,∠BAE=∠CAD=60°,
∴∠BAE+∠BAC=∠CAD+∠BAC,
∴∠CAE=∠BAD,
∴△AEC≌△ABD(SAS),
∴BD=EC;
②如图所示,过点D作DM⊥AE,交EA的延长线于点M,
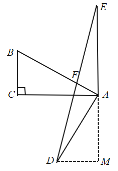
由旋转可得,AB=AE=2,AC=AD=![]() ,∠BAE=∠CAD=60°,
,∠BAE=∠CAD=60°,
∵∠BAC=30°,
∴∠CAE=∠BAE+∠BAC=90°,
∴∠CAM=90°,
∴∠DAM=30°,
∴在Rt△ADM中,DM=![]() AD=
AD=![]() ,AM=
,AM=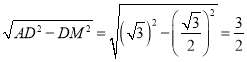 ,
,
∴EM=AE+AM=2+![]() =
=![]() ,
,
∴在Rt△DME中,DE=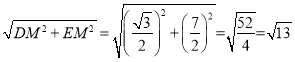 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目