题目内容
【题目】在平面直角坐标系中,![]() 的斜边
的斜边![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() ,把
,把![]() 先绕点
先绕点![]() 顺时针旋转
顺时针旋转![]() ,然后向下平移
,然后向下平移![]() 个单位,则点
个单位,则点![]() 的对应点
的对应点![]() 的坐标为________.
的坐标为________.

【答案】![]()
【解析】
根据直角三角形的性质和勾股定理可得BC,AB,利用直角三角形的面积可得AE,再利用射影定理易得BE,可得点A的坐标,根据旋转的性质易得D的坐标,再利用平移的性质可得结果.
作AE⊥BC,并作出把Rt△ABC先绕B点顺时针旋转180°后所得△DBC1,如图所示,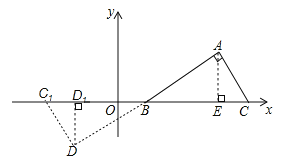
∵AC=2,∠ABC=30°,
∴BC=4
∴AB=2![]() ,
,
∴AE=![]() ,
,
∴BE=![]() ,
,
∵点B坐标为(1,0),
∴A点的坐标为(4,![]() ),
),
∵BE=3,
∴BD1=3,
∴D1坐标为(-2,0)
∴D坐标为(-2,-![]() ),
),
∵再向下平移2个单位,
∴D的坐标为(-2,-2-![]() ),
),
故答案是:(-2,-2-![]() ).
).

练习册系列答案
相关题目