题目内容
【题目】等边![]() 边长为
边长为![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,且
,且![]() 、
、![]() 分别于边
分别于边![]() 、
、![]() 交于点
交于点![]() 、
、![]() .
.
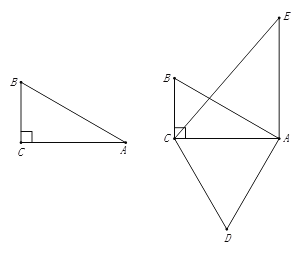
![]() 如图
如图![]() ,当点
,当点![]() 为
为![]() 的三等分点,且
的三等分点,且![]() 时,判断
时,判断![]() 的形状;
的形状;
![]() 如图
如图![]() ,若点
,若点![]() 在
在![]() 边上运动,且保持
边上运动,且保持![]() ,设
,设![]() ,四边形
,四边形![]() 面积的
面积的![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 如图
如图![]() ,若点
,若点![]() 在
在![]() 边上运动,且
边上运动,且![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 时,求
时,求![]() 的长.
的长.

【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据三等分点的定义,求得BP与PC的长,进而根据直角三角形中30度的锐角所对的直角边等于斜边的一半,即可求得BE的长,即可作出判断;
(2)分别表示出△ABC、△BPE、△PCF的面积,根据四边形AEPF的面积=△ABC的面积-△BPE的面积-△PCF的面积,即可求解;
(3)首先证明△BPE∽△CFP,根据相似三角形的对应边的比相等即可求得BP的长,进而即可求得PE的长.
![]() ∵点
∵点![]() 为
为![]() 的三等分点,
的三等分点,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴在直角![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 是等边三角形;
是等边三角形;
![]() 的面积是:
的面积是:![]() ;
;
![]() ,则
,则![]() .
.![]() ,
,![]() ,
,![]() .
.
则![]() 的面积是:
的面积是:![]() ,
,
![]() 的面积是:
的面积是:![]() .
.
∴四边形![]() 面积的
面积的![]() ;
;
即![]() ;
;
![]() ∵在
∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() .
.
∴![]() ,
,
解得:![]() 或
或![]() .
.
当![]() 时,在三角形
时,在三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
则![]() ;
;
当![]() 时,在三角形
时,在三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
则![]() 是等边三角形,∴
是等边三角形,∴![]() .
.
故![]() 或
或![]() .
.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目