题目内容
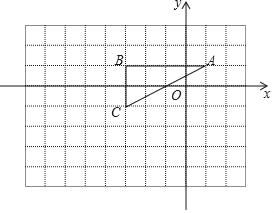
【题目】如图，
、
分别是正方形
的边
、
上的点，
，
、
相交于点
．下列结论：
；
；
与
成中心对称．其中，正确的结论有（ ）
A. 0个 B. 1个 C. 2个 D. 3个
【答案】C
【解析】
只要证明△BAF≌△ADE，推出BF＝AE,∠ABF＝∠DAE ,由∠DAE＋∠BAO＝90°，推出∠BAO＋∠ABO＝90°，推出AE⊥BF ,推出①②正确,因为△ABF绕对角线的交点顺时针旋转90°可得△ADE，所以△ABF与△DAE不成中心对称，由此即可判断.
∵四边形ABCD是正方形，∴AB＝AD＝CD，∠BAD＝∠D＝90°，∵CE＝DF，∴AF＝DE，在△BAF和△ADE中，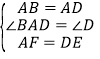
，∴△BAF≌△ADE，∴BF＝AE，∠ABF＝∠DAE，∵∠DAE＋∠BAO＝90°，∴∠BAO＋∠ABO＝90°，∴AE⊥BF，∴①②正确，∵△ABF绕对角线的交点顺时针旋转90°可得△ADE，∴△ABF与△DAE不成中心对称，故③错误，故答案选C.
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
