ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–”–“ΜΗώΒψ»ΐΫ«–ΈΘ§ΗΟ»ΐΫ«–ΈΒΡ»ΐΗωΕΞΒψΈΣΘΚAΘ®1Θ§1Θ©Θ§BΘ®©¹3Θ§1Θ©Θ§CΘ®©¹3Θ§©¹1Θ©Θ°
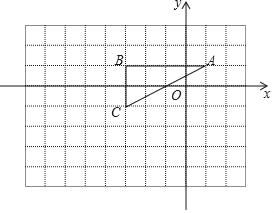
Θ®1Θ©»τΓςABCΒΡΆβΫ”‘≤ΒΡ‘≤–ΡΈΣPΘ§‘ρΒψPΒΡΉχ±ξΈΣ_____Θ§Γ―PΒΡΑκΨΕΈΣ_____ΘΜ
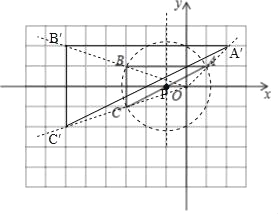
Θ®2Θ©»γΆΦΥυ ΨΘ§‘Ύ11ΓΝ8ΒΡΆχΗώΆΦΡΎΘ§“‘Ήχ±ξ‘≠ΒψOΒψΈΣΈΜΥΤ÷––ΡΘ§ΫΪΓςABCΑ¥œύΥΤ±»2ΘΚ1Ζ≈¥σΘ§AΓΔBΓΔCΒΡΕ‘”ΠΒψΖ÷±πΈΣA'ΓΔB'ΓΔC'Θ°ΔΌΜ≠≥ωΓςA'B'C'ΘΜΔΎΫΪΓςA'B'C'―Ίx÷αΖΫœρΤΫ“ΤΘ§–ηΤΫ“Τ_____ΗωΒΞΈΜ≥ΛΕ»Θ§Ρή ΙΒΟB'C'Υυ‘ΎΒΡ÷±œΏ”κΓ―Pœύ«–Θ°
ΓΨ¥πΑΗΓΩΘ®©¹1Θ§0Θ© ![]() 5©¹
5©¹![]() Μρ5+
Μρ5+![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©”…Χβ“βΩ…÷ΣΓςABC «÷±Ϋ«»ΐΫ«–ΈΘ§Ής≥ωΆβΫ”‘≤Φ¥Ω…ΘΜ
Θ®2Θ©άϊ”ΟΈΜΥΤΆΦ–ΈΒΡΕ®“εΚΆ–‘÷ Ής≥ωΆΦ–ΈΘ§‘ΌΗυΨίΤΫ“ΤΒΡΕ®“εΚΆ–‘÷ ΦΑ«–œΏΒΡ≈–Ε®Φ¥Ω…ΒΟΤΫ“ΤΒΡΨύάκΘ°
Θ®1Θ©ΓςABCΒΡΆβΫ”‘≤Γ―P»γΆΦΥυ Ψ
”…ΆΦΩ…÷ΣΘ§ΒψPΒΡΉχ±ξΈΣΘ®©¹1Θ§0Θ©ΓΔΑκΨΕΈΣ![]() =
=![]() Θ§
Θ§
Ι ¥πΑΗΈΣΘΚΘ®©¹1Θ§0Θ©ΓΔ![]() ΘΜ
ΘΜ
Θ®2Θ©»γΆΦΥυ ΨΘ§ΓςAΓδBΓδCΓδΦ¥ΈΣΥυ«σΘ°
ΫΪΓςAΓδBΓδCΓδœρ”“ΤΫ“Τ5©¹![]() Μρ5+
Μρ5+![]() ΗωΒΞΈΜBΓδCΓδΥυ‘ΎΒΡ÷±œΏ”κΓ―Pœύ«–Θ§
ΗωΒΞΈΜBΓδCΓδΥυ‘ΎΒΡ÷±œΏ”κΓ―Pœύ«–Θ§
Ι ¥πΑΗΈΣΘΚ5©¹![]() Μρ5+
Μρ5+![]() Θ°
Θ°

 Ωλά÷–Γ≤© ΩΙ°ΙΧ”κΧαΗΏœΒΝ–¥πΑΗ
Ωλά÷–Γ≤© ΩΙ°ΙΧ”κΧαΗΏœΒΝ–¥πΑΗ





