题目内容
2013年6月11日,“神舟”十号载人航天飞船发射成功!如图,飞船完成变轨后,就在离地球(⊙O)表面约350km的圆形轨道上运行.当飞船运行到某地(P点)的正上方(F点)时,从飞船上能看到地球表面最远的点Q(FQ是⊙O的切线).已知地球的半径约为6 400km.求:

(1)∠QFO的度数;(结果精确到0.01°)
(2)地面上P,Q两点间的距离(PQ的长).
(π取3.142,结果保留整数)

(1)∠QFO的度数;(结果精确到0.01°)
(2)地面上P,Q两点间的距离(PQ的长).
(π取3.142,结果保留整数)
解:(1)∵FQ是⊙O的切线,∴OQ⊥FQ,即∠OQF=90°。
∴在Rt△OQF中,OQ=6400,OF=OP+PF=6400+350=6750。
∴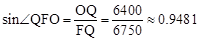 。
。
∴∠QFO≈71.46°。
答:∠QFO的度数约为71.46°。
(2)∵∠QFO=71.46°,∴∠FOQ=90°﹣71.46°=18.14°。
∴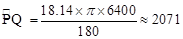 。
。
答:地面上P、Q两点间的距离约为2 071 km.
∴在Rt△OQF中,OQ=6400,OF=OP+PF=6400+350=6750。
∴
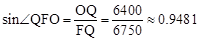 。
。∴∠QFO≈71.46°。
答:∠QFO的度数约为71.46°。
(2)∵∠QFO=71.46°,∴∠FOQ=90°﹣71.46°=18.14°。
∴
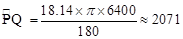 。
。答:地面上P、Q两点间的距离约为2 071 km.
试题分析:(1)根据切线的性质得OQ⊥FQ,则在Rt△OQF中,根据正弦的定义得到sin∠QFO≈0.9481,从而求出∠QFO。
(2)先计算出∠FOQ,然后根据弧长公式计算弧PQ的长。

练习册系列答案
相关题目

 ,求EF的长.
,求EF的长.
 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 cm.
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 cm.
 ,以A为圆心,1为半径的圆与边BC相切,则∠BAC的度数是 度.
,以A为圆心,1为半径的圆与边BC相切,则∠BAC的度数是 度.

 ,以B为圆心的弧与AD、DC相切,则阴影部分的面积是
,以B为圆心的弧与AD、DC相切,则阴影部分的面积是
 B.
B. C.
C. D.
D.

 ,CD=a,请用a表示⊙O的半径;
,CD=a,请用a表示⊙O的半径;