题目内容
【题目】如图1,O为正方形ABCD的中心,分别延长OA、OD到点F、E,使OF=2OA,OE=2OD,连接EF.将△EOF绕点O逆时针旋转α角得到△E1OF1(如图2). 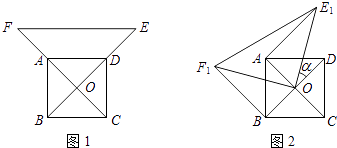
(1)探究AE1与BF1的数量关系,并给予证明;
(2)当α=30°时,求证:△AOE1为直角三角形.
【答案】
(1)解:AE1=BF1.
证明:∵O为正方形ABCD的中心,
∴OA=OD,
∵OF=2OA,OE=2OD,
∴OE=OF,
∵将△EOF绕点O逆时针旋转α角得到△E1OF1
∴OE1=OF1,
∵∠F1OB=∠E1OA,OA=OB,
∴△E1AO≌△F1BO,
∴AE1=BF1
(2)证明:∵取OE1中点G,连接AG,
∵∠AOD=90°,α=30°,
∴∠E1OA=90°﹣α=60°,
∵OE1=2OA,
∴OA=OG,
∴∠E1OA=∠AGO=∠OAG=60°,
∴AG=GE1,
∴∠GAE1=∠GE1A=30°,
∴∠E1AO=90°,
∴△AOE1为直角三角形.

【解析】(1)利用旋转不变量找到相等的角和线段,证得△E1AO≌△F1BO后即可证得结论;(2)利用已知角,得出∠GAE1=∠GE1A=30°,从而证明直角三角形.
【考点精析】本题主要考查了正方形的性质和旋转的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

练习册系列答案
相关题目