题目内容
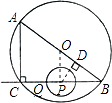
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s. 
(1)当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
(2)已知⊙O为△ABC的外接圆.若⊙P与⊙O相切,求t的值.
【答案】
(1)解:直线AB与⊙P相切,
如图,过P作PD⊥AB,垂足为D,
在Rt△ABC中,∠ACB=90°,
∵AC=6cm,BC=8cm,
∴AB=10cm,
∵P为BC中点,
∴PB=4cm,
∵∠PDB=∠ACB=90°,
∠PBD=∠ABC,
∴△PBD∽△ABC,
∴ ![]() ,
,
即 ![]() ,
,
∴PD=2.4(cm),
当t=1.2时,PQ=2t=2.4(cm),
∴PD=PQ,即圆心P到直线AB的距离等于⊙P的半径,
∴直线AB与⊙P相切
(2)解:∵∠ACB=90°,
∴AB为△ABC的外接圆的直径,
∴BO= ![]() AB=5cm,
AB=5cm,
连接OP,
∵P为BC中点,PO为△ABC的中位线,
∴PO= ![]() AC=3cm,
AC=3cm,
∵点P在⊙O内部,
∴⊙P与⊙O只能内切,
∴当⊙P在⊙O内部时:5﹣2t=3,
当⊙O在⊙P内部时2t﹣5=3,
∴t=1或4,
∴⊙P与⊙O相切时,t的值为1或4.
【解析】(1)根据已知求出AB=10cm,进而得出△PBD∽△ABC,利用相似三角形的性质得出圆心P到直线AB的距离等于⊙P的半径,即可得出直线AB与⊙P相切;(2)根据BO= ![]() AB=5cm,得出⊙P与⊙O只能内切,进而求出⊙P与⊙O相切时,t的值.
AB=5cm,得出⊙P与⊙O只能内切,进而求出⊙P与⊙O相切时,t的值.
【考点精析】根据题目的已知条件,利用勾股定理的概念和直线与圆的三种位置关系的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案