题目内容
【题目】有一张等腰三角形纸片,AB=AC=5,BC=3,小明将它沿虚线PQ剪开,得到△AQP和四边形BCPQ两张纸片(如图所示),且满足∠BQP=∠B,则下列五个数据 ![]() ,3,
,3, ![]() ,2,
,2, ![]() 中可以作为线段AQ长的有个.
中可以作为线段AQ长的有个. 
【答案】3
【解析】解:作CD∥PQ,交AB于D,如图所示: 则∠CDB=∠BQP,
∵AB=AC=5,
∴∠B=∠ACB,
∵∠BQP=∠B,
∴∠B=∠ACB=∠CDB,
∴CD=BC=3,△BCD∽△BAC,
∴ ![]() ,即
,即 ![]() ,
,
解得:BD= ![]() ,
,
∴AD=AB﹣BD= ![]() ,
,
∵CD∥PQ,
∴△APQ∽△ACD,
∴ ![]() ,即
,即 ![]() ,
,
解得:AP= ![]() AQ,
AQ,
当AQ= ![]() 时,AP=
时,AP= ![]() ×
× ![]() =
= ![]() >5,不合题意,舍去;
>5,不合题意,舍去;
当AQ=3时,AP= ![]() ×3=
×3= ![]() <5,符合题意;
<5,符合题意;
当AQ= ![]() 时,点P与C重合,不合题意,舍去;
时,点P与C重合,不合题意,舍去;
当AQ=2时,AP= ![]() ×2=
×2= ![]() <5,符合题意;
<5,符合题意;
当AQ= ![]() 时,AP=
时,AP= ![]() ×
× ![]() =
= ![]() <5,符合题意;
<5,符合题意;
综上所述:可以作为线段AQ长的有3个;
所以答案是:3.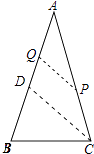
【考点精析】本题主要考查了等腰三角形的性质和相似三角形的判定与性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

【题目】校田园科技社团计划购进A、B两种花卉,两次购买每种花卉的数量以及每次的总费用如下表所示:
花卉数量(单位:株) | 总费用(单位:元) | ||
A | B | ||
第一次购买 | 10 | 25 | 225 |
第二次购买 | 20 | 15 | 275 |
(1)你从表格中获取了什么信息?(请用自己的语言描述,写出一条即可);
(2)A、B两种花卉每株的价格各是多少元?