题目内容
【题目】作图题:如图,直线AB,CD相交于点O,点P为射线OC上异于O的一个点.
(1)请用你手中的数学工具画出∠AOC的平分线OE;
(2)过点P画出(1)中所得射线OE的垂线PM(垂足为点M),并交直线AB于点N;
(3)请直接写出上述所得图形中的一对相等线段 .

【答案】(1)画图见解析;(2)画图见解析;(3)(3)OP,ON,(或者PM,NM)
【解析】分析:(1)利用尺规作图,
以O为圆心,任意长为半径作弧,与OA、OC交于两点,分别以这两点为圆心,以大于这两点之间距离的一半的长为半径作弧,两弧相交于一点,过O和这一点作一条以O为端点的射线OE即可;
(2)利用三角板进行作图即可;
(3)证明△OPM与△ONM全等即可得出相等的线段.
详解:如图:
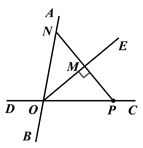
(1)(2)如图所示;
(3)∵PM⊥OE,
∴∠OMP=∠OMN=90°,
∵OE平分∠AOC,
∴∠POM=∠NOM,
∵OM=OM(公共边),
∴△OPM≌△ONM(ASA),
∴OP=ON,PM=NM,
故答案为:OP,ON(或者PM,NM).

练习册系列答案
相关题目