题目内容
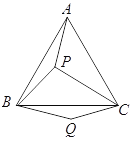
【题目】如图, ![]() 是等边三角形
是等边三角形![]() 内的一点,连结
内的一点,连结![]() 、
、![]() 、
、![]() ,以
,以![]() 为边作
为边作![]() 且
且![]() .连结
.连结![]() .
.
(1)观察并猜想![]() 与
与![]() 之间的大小关系,并证明你的结论.
之间的大小关系,并证明你的结论.
(2)若![]() ,
, ![]() ,
, ![]() ,连结
,连结![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
(3)在(2)的条件下,求![]() 的面积.
的面积.
【答案】(![]() )
)![]() ,证明见解析;(
,证明见解析;(![]() )
)![]() 为直角三角形,理由见解析;(
为直角三角形,理由见解析;(![]() )
)![]() .
.
【解析】试题分析:(1)通过证明△ABP≌△CBQ得出;(2)根据△BPQ是等边三角形求出PQ的长,再根据勾股定理逆定理可得△PQC是直角三角形;(3)过点B作BD垂直于CQ的延长线于点D,在△BDQ中求出DQ、BD的长,再求出CD,根据勾股定理求出BC的长,即可求出三角形ABC面积.
解:(1)AP=CQ,
理由:∵∠PBQ=60°,∠ABC=60°,
∴∠ABP+∠PBC=60°=∠CBQ+∠PBC,
∴∠ABP=∠CBQ,
在△ABP与△CBQ中,AB=CB,∠ABP=∠CBQ,BP=BQ,
∴△ABP≌△CBQ,
∴AP=CQ.
(2)∵BP=BQ,∠PBQ=60°,
∴△BPQ为等边三角形,
∴PQ=PB=4,
∵△ABP≌△CBQ,∴AP=CQ=3,
∵PQ2+CQ2=42+32=25=PC2,
∴△PQC为直角三角形.
(3)∵∠PQC=90°,∠PQB=60°,
∴∠BQC=150°,
过点B作BD垂直于CQ的延长线于点D,
∴∠BQD=30°,
∵BQ=4,∴BD=2,DQ=2![]() ,
,
∴CD=CQ+DQ=3+![]() ,
,
在Rt△BCD中,BC=![]() ,
,
∵△ABC为等边三角形,
∴S△ABC=![]() .
.

练习册系列答案
相关题目