题目内容
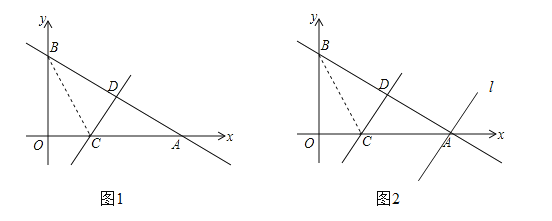
【题目】如图,在规格为8×8的边长为1个单位的正方形网格中(每个小正方形的边长为1),△ABC的三个顶点都在格点上,且直线m、n互相垂直.
(1)画出△ABC关于直线n的对称图形△A′B′C′;
(2)直线m上存在一点P,使△APB的周长最小;
①在直线m上作出该点P;(保留画图痕迹)
②△APB的周长的最小值为 .(直接写出结果)

【答案】(1)详见解析;(2)①详见解析;②![]() .
.
【解析】
(1)根据轴对称的性质,可作出△ABC关于直线n的对称图形△A′B′C′;
(2)①作点B关于直线m的对称点B',连接B'A与x轴的交点为点P;
②由△ABP的周长=AB+AP+BP=AB+AP+B'P,则当AP与PB'共线时,△APB的周长有最小值.
解:(1)如图△A′B′C′为所求图形.
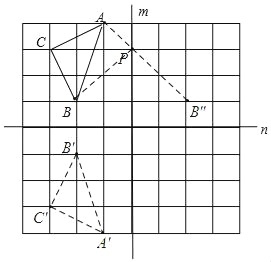
(2)①如图:点P为所求点.
②∵△ABP的周长=AB+AP+BP=AB+AP+B'P
∴当AP与PB'共线时,△APB的周长有最小值.
∴△APB的周长的最小值AB+AB'=![]() +3
+3![]()
故答案为:![]() +3
+3![]()

练习册系列答案
相关题目