题目内容
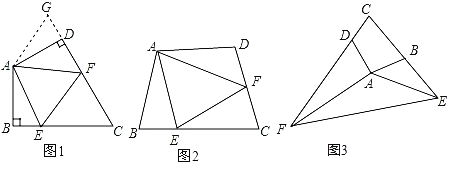
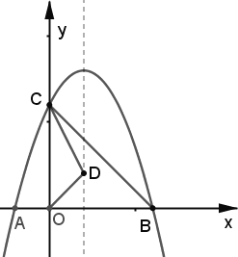
【题目】如图,△ABC中,∠ACB=90°,AC=CB=2,以BC为边向外作正方形BCDE,动点M从A点出发,以每秒1个单位的速度沿着A→C→D的路线向D点匀速运动(M不与A、D重合);过点M作直线l⊥AD,l与路线A→B→D相交于N,设运动时间为t秒:
(1)填空:当点M在AC上时,BN= (用含t的代数式表示);
(2)当点M在CD上时(含点C),是否存在点M,使△DEN为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由;
(3)过点N作NF⊥ED,垂足为F,矩形MDFN与△ABD重叠部分的面积为S,求S的最大值.
【答案】(1)BN=2![]() ﹣
﹣![]() t;(2)当t=4﹣
t;(2)当t=4﹣![]() 或t=3或t=2时,△DNE是等腰三角形;(3)当t=
或t=3或t=2时,△DNE是等腰三角形;(3)当t=![]() 时,S取得最大值
时,S取得最大值![]() .
.
【解析】
(1)由等腰直角三角形的性质知AB=2![]() ,MN=AM=t,AN=
,MN=AM=t,AN=![]() ﹣AM=
﹣AM=![]() ﹣t,据此可得;
﹣t,据此可得;
(2)先得出MN=DM=4﹣t,BP=PN=t﹣2,PE=4﹣t,由勾股定理得出NE=![]() ,再分DN=DE,DN=NE,DE=NE三种情况分别求解可得;
,再分DN=DE,DN=NE,DE=NE三种情况分别求解可得;
(3)分0≤t<2和2≤t≤4两种情况,其中0≤t<2重合部分为直角梯形,2≤t≤4时重合部分为等腰直角三角形,根据面积公式得出面积的函数解析式,再利用二次函数的性质求解可得.
(1)如图1,
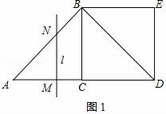
∵∠ACB=90°,AC=BC=2,
∴∠A=∠ABC=45°,AB=2![]() ,
,
∵AM=t,∠AMN=90°,
∴MN=AM=t,AN=![]() AM=
AM=![]() t,
t,
则BN=AB﹣AN=![]()
故答案为:![]()
(2)如图2,
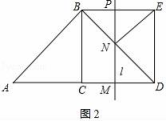
∵AM=t,AC=BC=CD=2,∠BDC=∠DBE=45°,
∴DM=MN=AD﹣AM=4﹣t,
∴DN=![]() DM=
DM=![]() (4﹣t),
(4﹣t),
∵PM=BC=2,
∴PN=2﹣(4﹣t)=t﹣2,
∴BP=t﹣2,
∴PE=BE﹣BP=2﹣(t﹣2)=4﹣t,
则NE=![]() ,
,
∵DE=2,
∴①若DN=DE,则![]() (4﹣t)=2,解得t=4﹣
(4﹣t)=2,解得t=4﹣![]() ;
;
②若DN=NE,则![]() (4﹣t)=
(4﹣t)=![]() ,解得t=3;
,解得t=3;
③若DE=NE,则2=![]() ,解得t=2或t=4(点N与点E重合,舍去);
,解得t=2或t=4(点N与点E重合,舍去);
综上,当t=4﹣![]() 或t=3或t=2时,△DNE是等腰三角形.
或t=3或t=2时,△DNE是等腰三角形.
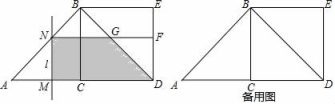
(3)①当0≤t<2时,如图3,
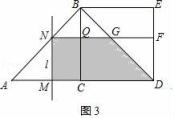
由题意知AM=MN=t,
则CM=NQ=AC﹣AM=2﹣t,
∴DM=CM+CD=4﹣t,
∵∠ABC=∠CBD=45°,∠NQB=∠GQB=90°,
∴NQ=BQ=QG=2﹣t,
则NG=4﹣2t,
∴![]()
当t=![]() 时,S取得最大值
时,S取得最大值![]() ;
;
②当2≤t≤4时,如图4,
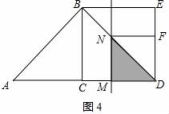
∵AM=t,AD=AC+CD=4,
∴DM=AD﹣AM=4﹣t,
∵∠DMN=90°,∠CDB=45°,
∴MN=DM=4﹣t,
∴S=![]() (4﹣t)2=
(4﹣t)2=![]() (t﹣4)2,
(t﹣4)2,
∵2≤t≤4,
∴当t=2时,S取得最大值2;
综上,当t=![]() 时,S取得最大值
时,S取得最大值![]() .
.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案