题目内容
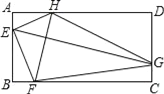
【题目】如图,△ABC≌△ADE,∠DAC=60 ![]() ,∠BAE=100
,∠BAE=100 ![]() ,BC,DE相交于点F,则∠DFB度数是( )
,BC,DE相交于点F,则∠DFB度数是( )
A.15 ![]()
B.20 ![]()
C.25 ![]()
D.30 ![]()
【答案】B
【解析】∵△ABC≌△ADE,
∴∠B=∠D,∠BAC=∠DAE,
又∠BAD=∠BAC-∠CAD,∠CAE=∠DAE-∠CAD,
∴∠BAD=∠CAE,
∵∠DAC=60°,∠BAE=100°,
∴∠BAD= ![]() (∠BAE-∠DAC)=
(∠BAE-∠DAC)= ![]() ×(100°-60°)=20°,
×(100°-60°)=20°,
在△ABG和△FDG中,∵∠B=∠D,∠AGB=∠FGD,
∴∠DFB=∠BAD=20°,
故答案为:B.
根据全等三角形的性质得出∠B=∠D,∠BAC=∠DAE,再证明∠BAD=∠CAE,求出∠BAD的度数,再根据△ABG和△FDG的内角和都等于180°,证得∠DFB=∠BAD,即可得出结果。

练习册系列答案
相关题目