题目内容
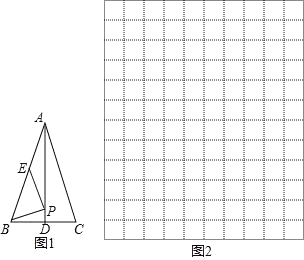
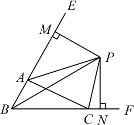
【题目】如图,在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP.
(1)求证:PA平分∠BAC的外角∠CAM;
(2)过点C作CE⊥AP,E是垂足,并延长CE交BM于点D.求证:CE=ED.
【答案】(1)见解析;(2)见解析
【解析】
(1)过P作PT⊥BC于T,PS⊥AC于S,PQ⊥BA于Q,根据角平分线性质求出PQ=PS=PT,根据角平分线性质得出即可;
(2)根据ASA求出△AED≌△AEC即可.
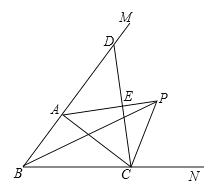
解:证明:(1)过P作PT⊥BC于T,PS⊥AC于S,PQ⊥BA于Q,如图,
∵在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,
∴PQ=PT,PS=PT,
∴PQ=PS,
∴AP平分∠DAC,
即PA平分∠BAC的外角∠CAM;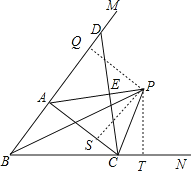
(2)∵PA平分∠BAC的外角∠CAM,
∴∠DAE=∠CAE,
∵CE⊥AP,
∴∠AED=∠AEC=90°,
在△AED和△AEC中,
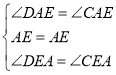 ,
,
∴△AED≌△AEC(ASA),
∴CE=ED.

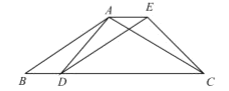
【题目】如图 1,在等腰△ABC 中,AB=AC,点 D,E 分别为 BC,AB 的中点,连接 AD.在线段 AD 上任取一点 P,连接 PB,PE.若 BC=4,AD=6,设 PD=x(当点 P 与点 D 重合时,x 的值为 0),PB+PE=y.
小明根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究. 下面是小明的探究过程,请补充完整:
(1)通过取点、画图、计算,得到了 x 与 y 的几组值,如下表:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y | 5.2 | 4.2 | 4.6 | 5.9 | 7.6 | 9.5 |
说明:补全表格时,相关数值保留一位小数.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.236)
≈2.236)
(2)建立平面直角坐标系(图 2),描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)求函数 y 的最小值(保留一位小数),此时点 P 在图 1 中的什么位置.