题目内容
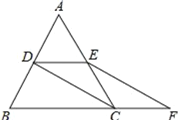
【题目】如图，已知
中，
，过点
作
，过
作
交
于
，连接
．
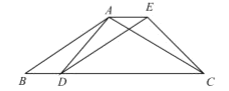
（1）求证：
；
（2）若
，
，
，求平行四边形
的面积．
【答案】（1）见详解；（2）
.
【解析】
（1）由AB=AC，则∠B=∠ACD，由
，
，则四边形ABDE是平行四边形，则AE=BD，∠EAC=∠ACD=∠B，根据SAS即可得到结论成立；
（2）过点A作AF⊥BC于点F，设AF=x，则AB=2x，DF=x，利用勾股定理建立方程，即可求出x，然后计算面积即可.
（1）证明：∵在
中，
，
∴∠B=∠ACD，
∵，
∴∠EAC=∠ACD=∠B，
∵，
∴四边形ABDE是平行四边形，
∴AE=BD，
∴
（SAS）；
（2）解：如图，过点A作AF⊥BC于点F，
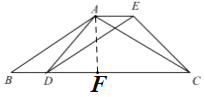
∴△ABF和△ADF是直角三角形，设AF=x，
∵
，
，
∴AB=2x，DF=x，
∵BF=BD+DF，
∴
，
整理得：
，
解得：
，
，
经检验，均为方程的根，
∵
，不符合题意，舍去；
∴
，
∴平行四边形
的面积为：
；
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
