题目内容
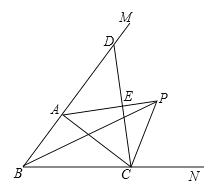
【题目】如图,△![]() 中,
中,![]() 、
、![]() 的角平分线
的角平分线![]() 、
、![]() 交于点
交于点![]() ,延长
,延长![]() 、
、![]() ,
,![]() ,
,![]() ,则下列结论中正确的个数是( )
,则下列结论中正确的个数是( )
①CP平分∠ACF; ②∠ABC+2∠APC=180°;
③∠ACB=2∠APB; ④若PM⊥BE,PN⊥BC,则AM+CN=AC;
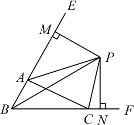
A.1个B.2个C.3个D.4个
【答案】D
【解析】
①作PD⊥AC于D.由角平分线的性质得出PM=PN,PM=PD,得出PM=PN=PD,即可得出①正确;
②首先证出∠ABC+∠MPN=180°,证明Rt△PAM≌Rt△PAD(HL),得出∠APM=∠APD,同理:Rt△PCD≌Rt△PCN(HL),得出∠CPD=∠CPN,即可得出②正确;
③由角平分线和三角形的外角性质得出∠CAE=∠ABC+∠ACB,∠PAM=![]() ∠ABC+∠APB,得出∠ACB=2∠APB,③正确;
∠ABC+∠APB,得出∠ACB=2∠APB,③正确;
④由全等三角形的性质得出AD=AM,CD=CN,即可得出④正确;即可得出答案.
解:①作PD⊥AC于D.
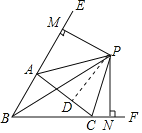
∵PB平分∠ABC,PA平分∠EAC,PM⊥BE,PN⊥BF,
∴PM=PN,PM=PD,
∴PM=PN=PD,
∴点P在∠ACF的角平分线上,故①正确;
②∵PM⊥AB,PN⊥BC,
∴∠ABC+90°+∠MPN+90°=360°,
∴∠ABC+∠MPN=180°,
在Rt△PAM和Rt△PAD中,
![]() ,
,
∴Rt△PAM≌Rt△PAD(HL),
∴∠APM=∠APD,
同理:Rt△PCD≌Rt△PCN(HL),
∴∠CPD=∠CPN,
∴∠MPN=2∠APC,
∴∠ABC+2∠APC=180°,②正确;
③∵PA平分∠CAE,BP平分∠ABC,
∴∠CAE=∠ABC+∠ACB,∠PAM=![]() ∠ABC+∠APB,
∠ABC+∠APB,
∴∠ACB=2∠APB,③正确;
④∵Rt△PAM≌Rt△PAD(HL),
∴AD=AM,
同理:Rt△PCD≌Rt△PCN(HL),
∴CD=CN,
∴AM+CN=AD+CD=AC,④正确;
故选:D.