题目内容
【题目】如图,抛物线y=﹣![]() x2+
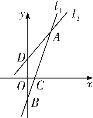
x2+![]() x+2与x轴相交于A、B两点,与y轴相交于点C,点D在抛物线上,且CD∥AB.AD与y轴相交于点E,过点E的直线PQ平行于x轴,与拋物线相交于P,Q两点,则线段PQ的长为_____.
x+2与x轴相交于A、B两点,与y轴相交于点C,点D在抛物线上,且CD∥AB.AD与y轴相交于点E,过点E的直线PQ平行于x轴,与拋物线相交于P,Q两点,则线段PQ的长为_____.
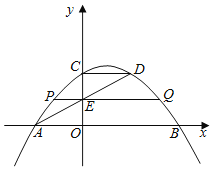
【答案】2![]()
【解析】
利用二次函数图象上点的坐标特征可求出点A,B,C,D的坐标,由点A,D的坐标,利用待定系数法可求出直线AD的解析式,利用一次函数图象上点的坐标特征可求出点E的坐标,再利用二次函数图象上点的坐标特征可得出点P,Q的坐标,进而可求出线段PQ的长.
解:当y=0时,﹣![]() x2+
x2+![]() x+2=0,
x+2=0,
解得:x1=﹣2,x2=4,
∴点A的坐标为(﹣2,0);
当x=0时,y=﹣![]() x2+
x2+![]() x+2=2,
x+2=2,
∴点C的坐标为(0,2);
当y=2时,﹣![]() x2+
x2+![]() x+2=2,
x+2=2,
解得:x1=0,x2=2,
∴点D的坐标为(2,2).
设直线AD的解析式为y=kx+b(k≠0),
将A(﹣2,0),D(2,2)代入y=kx+b,得:
![]() 解得:
解得: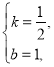
∴直线AD的解析式为y=![]() x+1.
x+1.
当x=0时,y=![]() x+1=1,
x+1=1,
∴点E的坐标为(0,1).
当y=1时,﹣![]() x2+
x2+![]() x+2=1,
x+2=1,
解得:x1=1﹣![]() ,x2=1+
,x2=1+![]() ,
,
∴点P的坐标为(1﹣![]() ,1),点Q的坐标为(1+
,1),点Q的坐标为(1+![]() ,1),
,1),
∴PQ=1+![]() ﹣(1﹣
﹣(1﹣![]() )=2
)=2![]() .
.
故答案为:2![]() .
.

【题目】某公司计划投入50万元,开发并生产甲乙两种产品,根据市场调查预计甲产品的年获利y1(万元)与投入资金x(万元)成正比例,乙产品的年获利y2(万元)与投入资金x(万元)的平方成正比例,设该公司投入乙产品x(万元),两种产品的年总获利为y万元(x≥0),得到了表中的数据.
x(万元) | 20 | 30 |
y(万元) | 10 | 13 |
(1)求y与x的函数关系式;
(2)该公司至少可获得多少利润?请你利用所学的数学知识对该公司投入资金的分配提出合理化建
议,使他能获得最大利润,并求出最大利润是多少?
(3)若从年总利润扣除投入乙产品资金的a倍(a≤1)后,剩余利润随x增大而减小,求a的取值
范围.
【题目】某小区超市一段时间每天订购80个面包进行销售,每售出1个面包获利润0.5元,未售出的每个亏损0.3元.(1)若今后每天售出的面包个数用x(0<x≤80)表示,每天销售面包的利润用y(元)表示,写出y与x的函数关系式;
(2)小明连续m天对该超市的面包销量进行统计,并制成了频数分别直方图(每个组距包含左边的数,但不包含右边的数)和扇形统计图,如图1、图2所示,请结合两图提供的信息,解答下列问题:
①m的值为 ;
②求在m天内日销售利润少于32元的天数;
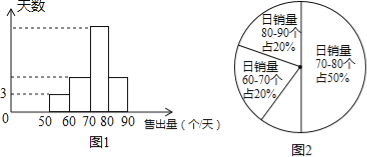
(3)如图(2)中m天内日销售面包个数在70≤x<80这个组内的销售情况如表:
销售量/个 | 70 | 72 | 73 | 75 | 78 | 79 |
天数 | 1 | 2 | 3 | 4 | 3 | 2 |
请计算该组内平均每天销售面包的个数.