题目内容
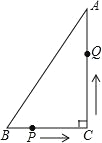
【题目】如图,在Rt△ABC中,AC=8cm,BC=6cm,P点在BC上,从B点到C点运动(不包括 C点),点 P运动的速度为1cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为2cm/s,若点 P、Q 分别从B、C 同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.
(1)当 t 为何值时,P、Q 两点的距离为 4![]() cm?
cm?
(2)请用配方法说明,点P运动多少时间时,四边形BPQA的面积最小?最小面积是多少?
【答案】(1) 2或![]() ;(2) 3秒,15cm2.
;(2) 3秒,15cm2.
【解析】
(1)根据勾股定理PC2+CQ2=PQ2,便可求出经过2或![]() s后,P、Q两点的距离为4
s后,P、Q两点的距离为4![]() cm;(2)根据三角形的面积公式S△PCQ=
cm;(2)根据三角形的面积公式S△PCQ=![]() ×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.
×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.
:(1)∵在Rt△ABC中,AC=8cm,BC=6cm,
∴AB=10cm,
设经过ts后,P、Q两点的距离为4![]() cm,
cm,
ts后,PC=6-t cm,CQ=2t cm,
根据勾股定理可知PC2+CQ2=PQ2,
代入数据(6-t)2+(2t)2=(4![]() )2;
)2;
解得t=2或t=![]() ,
,
故t为2或![]() 时,P、Q两点的距离为4
时,P、Q两点的距离为4![]() cm;
cm;
(2)设经过ts后,△PCQ的面积最大,则此时四边形BPQA的面积最小,
ts后,PC=6-tcm,CQ=2t cm,
S△PCQ=![]() ×PC×CQ=
×PC×CQ=![]() ×(6-t)×2t=-t2+6t
×(6-t)×2t=-t2+6t
当t=-![]() 时,即t=3s时,△PCQ的面积最大,
时,即t=3s时,△PCQ的面积最大,
即S△PCQ=![]()
×PC×CQ=![]() ×(6-3)×6=9(cm2),
×(6-3)×6=9(cm2),
∴四边形BPQA的面积最小值为:S△ABC-S△PCQ最大=![]() ×6×8-9=15(cm2),
×6×8-9=15(cm2),
当点P运动3秒时,四边形BPQA的面积最小为:15cm2.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目