题目内容
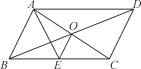
【题目】如图,ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连结OE.下列结论:
BC,连结OE.下列结论:
①∠CAD=30°;②SABCD=AB·AC;③OB=AB;④OE=![]() BC,成立的结论有______.(填序号)
BC,成立的结论有______.(填序号)
【答案】①②④
【解析】
由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=![]() BC,得到AE=
BC,得到AE=![]() BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到SABCD=ABAC,故②正确,根据AB=
BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到SABCD=ABAC,故②正确,根据AB=![]() BC,OB=
BC,OB=![]() BD,且BD>BC,得到AB≠OB,故③错误;根据三角形的中位线定理得到OE=
BD,且BD>BC,得到AB≠OB,故③错误;根据三角形的中位线定理得到OE=![]() AB,于是得到OE=
AB,于是得到OE=![]() BC,故④正确.
BC,故④正确.
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=![]() BC,
BC,
∴AE=![]() BC,
BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴SABCD=ABAC,故②正确,
∵AB=![]() BC,OB=
BC,OB=![]() BD,
BD,
∵BD>BC,
∴AB≠OB,故③错误;
∵CE=BE,CO=OA,
∴OE=![]() AB,
AB,
∴OE=![]() BC,故④正确.
BC,故④正确.
故答案为:①②④.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目