题目内容
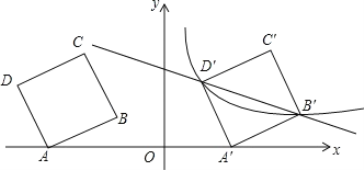
【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(-6,0),D(-7,3),点B、C在第二象限内.
(1)点B的坐标 ;
(2)将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请求出符合题意的点P、Q的坐标;若不存在,请说明理由.

【答案】(1)(![]() );(2)t=9,
);(2)t=9,![]() ;(3)点P、Q的坐标为:P(
;(3)点P、Q的坐标为:P(![]() ,0)、Q(
,0)、Q(![]() ,4)或P(7,0)、Q(3,2)或P(-7,0)、Q(-3,-2).
,4)或P(7,0)、Q(3,2)或P(-7,0)、Q(-3,-2).
【解析】
(1)过点D作DE⊥x轴于点E,过点B作BF⊥x轴于点F,由正方形的性质结合同角的余角相等即可证出△ADE≌△BAF,从而得出DE=AF,AE=BF,再结合点A、D的坐标即可求出点B的坐标;
(2)设反比例函数为![]() ,根据平行的性质找出点B′、D′的坐标,再结合反比例函数图象上点的坐标特征即可得出关于k、t的二元一次方程组,解方程组解得出结论;
,根据平行的性质找出点B′、D′的坐标,再结合反比例函数图象上点的坐标特征即可得出关于k、t的二元一次方程组,解方程组解得出结论;
(3)假设存在,设点P的坐标为(m,0),点Q的坐标为(n,![]() ).分B′D′为对角线或为边考虑,根据平行四边形的性质找出关于m、n的方程组,解方程组即可得出结论.
).分B′D′为对角线或为边考虑,根据平行四边形的性质找出关于m、n的方程组,解方程组即可得出结论.
解:(1)过点D作DE⊥x轴于点E,过点B作BF⊥x轴于点F,如图1所示.

∵四边形ABCD为正方形,
∴AD=AB,∠BAD=90°,
∵∠EAD+∠ADE=90°,∠EAD+∠BAF=90°,
∴∠ADE=∠BAF.
在△ADE和△BAF中,有
 ,
,
∴△ADE≌△BAF(AAS),
∴DE=AF,AE=BF.
∵点A(-6,0),D(-7,3),
∴DE=3,AE=1,
∴点B的坐标为(-6+3,0+1),即(-3,1).
故答案为:(-3,1).
(2)设反比例函数为![]() ,
,
由题意得:点B′坐标为(-3+t,1),点D′坐标为(-7+t,3),
∵点B′和D′在该比例函数图象上,
∴![]() ,
,
解得:t=9,k=6,
∴反比例函数解析式为![]() .
.
(3)假设存在,设点P的坐标为(m,0),点Q的坐标为(n,![]() ).
).
以P、Q、B′、D′四个点为顶点的四边形是平行四边形分两种情况:

①B′D′为对角线时,
∵四边形B′PD′Q为平行四边形,
∴ ,解得:
,解得: ,
,
∴P(![]() ,0),Q(
,0),Q(![]() ,4);
,4);
②当B′D′为边时.
∵四边形PQB′D′为平行四边形,
∴ ,解得:
,解得:![]() ,
,
∴P(7,0),Q(3,2);
∵四边形B′QPD′为平行四边形,
∴ ,解得:
,解得:![]() .
.
综上可知:存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形,符合题意的点P、Q的坐标为:P(![]() ,0)、Q(
,0)、Q(![]() ,4)或P(7,0)、Q(3,2)或P(-7,0)、Q(-3,-2).
,4)或P(7,0)、Q(3,2)或P(-7,0)、Q(-3,-2).

【题目】如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,AD=![]() ,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )

A. ![]() B. 2C. 1D. 3
B. 2C. 1D. 3
【题目】均匀的正四面体的各面依次标有![]() 四个数字
四个数字![]() 小明做了60次投掷试验,结果统计如下:
小明做了60次投掷试验,结果统计如下:
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
![]() 计算上述试验中“4朝下”的频率是多少?
计算上述试验中“4朝下”的频率是多少?
![]() “根据试验结果,投掷一次正四面体,出现2朝下的概率是
“根据试验结果,投掷一次正四面体,出现2朝下的概率是![]() ”的说法正确吗?为什么?
”的说法正确吗?为什么?