��Ŀ����
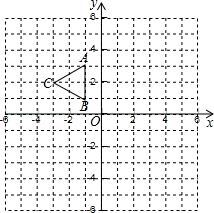
��ͼ���ı���ABCD�У��Խ���AC��BD�ཻ��O���ڢ�AB��CD����AO��CO����AD��BC������ѡȡ������Ϊ���������ı���ABCD��ƽ���ı��Ρ�Ϊ���۹������⣮
��1���Ԣ٢���Ϊ�������ɵ������������������ǣ���֤���������ǣ���ٳ�������
��2��д��������ɵ����������еļ����⣬���ٳ���������˵������������д�ɡ����������ô����������ʽ��
��1������ƽ�еó����������Σ��Ƴ�����ʽ���������OB=OD��������ȫ�ȣ�����ƽ���ı��ε��ж��Ƴ����ɡ�
��2�����ݵ������κ�ƽ���ı��ε��ж��жϼ��ɡ�
������������1������ƽ�еó����������Σ��Ƴ�����ʽ���������OB=OD��������ȫ�ȣ�����ƽ���ı��ε��ж��Ƴ����ɡ�
��2�����ݵ������κ�ƽ���ı��ε��ж��жϼ��ɡ�
�⣺��1���Ԣ٢���Ϊ�������ɵ������������⣬֤�����£�
��AB��CD�� ���AOB�ס�COD���� ��
��
��AO=OC����OB=OD��
���ı���ABCD��ƽ���ı��Ρ�
��2���������ݢ٢���Ϊ�������ɵ������Ǽ����⣬���������һ��Ա�ƽ�У�����һ��Ա���ȵ��ı���ʱƽ���ı��Σ���������η��ϣ�������ƽ���ı��Σ�
�������ݢڢ���Ϊ�������ɵ������Ǽ����⣬�������һ���ı���ABCD�ĶԽ��߽���O����OA=OC��AD=BC����ô����ı���ʱƽ���ı��Σ���ͼ��������֪�����Ƴ�OB=OD��AD��BC��AB=DC�����ı��β���ƽ���ı��Ρ�

��ͼ1���õ�һ�������������������������ͼ��ͼ2�����丩��ͼ�ǣ� ��
A�� | B�� | C�� | D�� |

 ��
��