题目内容
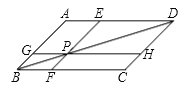
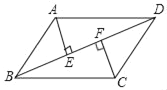
【题目】如图,平行四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F,连结AF、CE.
(1)求证:四边形AECF是平行四边形;
(2)若AB=6,AD=2![]() ,∠ABD=30°,求四边形AECF的面积.
,∠ABD=30°,求四边形AECF的面积.
【答案】(1)证明见解析;(2)6![]() .
.
【解析】
(1)由四边形ABCD是平行四边形,可得AB=CD,AB∥CD,又由AE⊥BD,CF⊥BD,即可得AE∥CF,∠AEB=∠CFD=90°,然后利用AAS证得△AEB≌△CFD,即可得AE=CF,由有一组对边相等且平行的四边形是平行四边形,即可证得四边形AECF是平行四边形.
(2)根据直角三角形中30°的角所对的直角边为斜边的一半,求出AE和BE的长,再根据勾股定理求出DE的长,从而求出DF和EF的长,根据S平行四边形AECF=底![]() 高计算即可;
高计算即可;
(1)连接AF、EC.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEB=∠CFD=90°,
在△AEB和△CFD中,
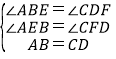 ,
,
∴△AEB≌△CFD(AAS),
∴AE=CF,
∴四边形AECF是平行四边形.
(2)在Rt△ABE中,∵AB=6,∠ABD=30°,
∴AE=![]() AB=3,BE=
AB=3,BE=![]() AE=3
AE=3![]() ,
,
在Rt△ADE中,AD=2![]() ,
,
DE=![]()
∵△AEB≌△CFD,
∴BE=DF=3![]() ,
,
∴EF=DE-DF=2![]() ,
,
∴S平行四边形AECF=![]() =6
=6![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】核桃和枣是我省著名的农特产,它们营养丰富,有益人体健康,深受老百姓喜爱。某超市从农贸批发市场批发核桃和枣进行零售,批发价和零售价格如下表所示:
名称 | 核桃 | 枣 |
批发价(元/ | 12 | 9 |
零售价(元/ | 18 | 12 |
请解答下列问题.
(1)第一天,该超市从批发市场批发核桃和枣共350![]() ,用去了3600元钱,求当天核桃和枣各批发多少kg?
,用去了3600元钱,求当天核桃和枣各批发多少kg?
(2)第二天,该超市用3600元钱仍然批发核桃和枣(批发价和零售价不变),要想将第二天批发的核桃和枣全部售完后,所获利润不低于40%,则该超市第二天至少批发核桃多少kg?