题目内容
【题目】如图，点A是反比例函数y1= 
（x＞0）图象上一点，过点A作x轴的平行线，交反比例函数y2= 
（x＞0）的图象于点B，连接OA，OB，若△OAB的面积为2，则k2﹣k1的值为（ ）
A.﹣2
B.2
C.﹣4
D.4
【答案】D
【解析】解：延长BA交y轴于点D，如图所示．
∵点A、B是函数y= 
（x＞0）和y= 
（x＞0）图象上一点，
∴S△AOD= 
k1，S△OBD= k2，
∴S△OAB=S△BOD﹣S△AOD=2．
∴ k2﹣ k1=2，
则k2﹣k1=4．
所以答案是：D．
【考点精析】本题主要考查了比例系数k的几何意义的相关知识点，需要掌握几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题．
练习册系列答案
相关题目
【题目】某校数学兴趣小组成员小华对本班上学期期末考试数学成绩（成绩取整数，满分为100分）作了统计分析，绘制成如下频数分布直方图和频数、频率分布表．请你根据图表提供的信息，解答下列问题：
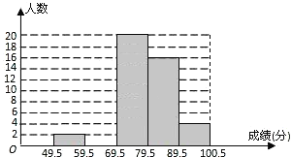
分组 | 49.5～59.5 | 59.5～69.5 | 69.5～79.5 | 79.5～89.5 | 89.5～100.5 | 合计 |
频数 | 2 |
| 20 | 16 | 4 | 50 |
频率 | 0.04 | 0.16 | 0.40 | 0.32 |
| 1 |
（1）频数、频率分布表中
，
；
（2）补全频数分布直方图；
（3）数学老师准备从不低于90分的学生中选1人介绍学习经验，那么取得了93分的小华被选上的概率是多少？
【题目】某一天，水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克，后再到水果市场去卖，已知猕猴桃和芒果当天的批发价和零售价如表所示：
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
他购进的猕猴桃和芒果各多少千克？
如果猕猴桃和芒果全部卖完，他能赚多少钱？
