Question

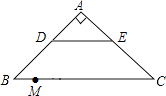
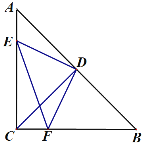
【题目】如图1，将矩形纸片ABCD沿对角线BD向上折叠，点C落在点E处，BE交AD于点F.

(1)求证：△BDF是等腰三角形；

(2)如图2，过点D作DG∥BE，交BC于点G，连接FG交BD于点O.

①判断四边形BFDG的形状，并说明理由；

②若AB＝6，AD＝8，求FG的长．

图1

图2

Answer 1

【答案】（1）详见解析；（2）①四边形BFDG是菱形；②.

【解析】

1）根据两直线平行内错角相等及折叠特性判断；

（2）①根据已知矩形性质及第一问证得邻边相等判断；

②根据折叠特性设未知边，构造勾股定理列方程求解．

(1)证明：如图1，由折叠得，∠DBC＝∠DBE.∵AD∥BC∴∠DBC＝∠BDA

∴∠BDA＝∠DBE∴BF＝DF∴△BDF是等腰三角形．

(2)①四边形BFDG是菱形，理由如下：如图2

∵AD∥BC.DG∥BF.∴四边形BFDG是平行四边形，

又∵BF＝DF，∴四边形BFDG是菱形．

②∵四边形BFDG是菱形．∴FG⊥BD.BO＝BD.FO＝FG

∵AB＝6，AD＝8∴BD＝10.∴BO＝5.设DF＝x，

则AF＝8－x在Rt△ABF中，62＋(8－x)2＝x2

解得x＝，在Rt△BOF中，∴FO＝＝∴FG＝2FO＝.