题目内容
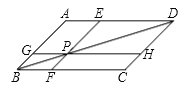
【题目】如图，在ABCD中，过对角线BD上点P作直线EF，GH分别平行于AB，BC，那么图中共有（ ）对面积相等平行四边形．
A. 1对B. 2对C. 3对D. 4对
【答案】C
【解析】
平行四边形的对角线将平行四边形分成两个面积相等的三角形．所以三角形ABD的面积等于三角形BCD的面积．三角形BFP的面积等于BGP的面积，三角形PED的面积等于三角形HPD的面积，从而可得到四边形PFCH的面积等于四边形AGPE的面积，同时加上一个公共的平行四边形，可以得出答案有三个．
∵ABCD为平行四边形，BD为对角线，∴△ABD的面积等于△BCD的面积，同理△BFP的面积等于△BGP的面积，△PED的面积等于△HPD的面积．
∵△BCD的面积减去△BFP的面积和PHD的面积等于平行四边形PFCH的面积，△ABD的面积减去△GBD和△EPD的面积等于平行四边形AGPE的面积，∴平行四边形PFCH的面积=平行四边形AGPE的面积，∴同时加上平行四边形PHDE和BFPG，可以得出平行四边形AGHD面积和平行四边形EFCD面积相等，平行四边形ABFE和平行四边形BCHG面积相等．
所以有3对面积相等的平行四边形．
故选C．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
