Question

【题目】如图，在ABCD中，AB＝2BC，M是AB的中点，则∠CMD（　　）

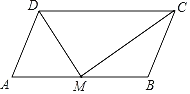
A.是锐角B.是直角

C.是钝角D.度数不能确定

Answer 1

【答案】B

【解析】

根据平行四边形ABCD中，AB＝2BC，M是AB的中点，易得AD＝AM＝BM＝BC，继而证得DM，CM分别是∠ADC与∠BCD的角平分线，继而证得结论．

证明：如图，∵四边形ABCD是平行四边形，

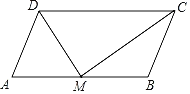
∴AB＝CD（平行四边形对边相等），

∵AB＝2BC，M是AB的中点，

∴AD＝BC＝AM＝BM，

∴∠ADM＝∠AMD，∠BCM＝∠BMC，

∵AB∥CD（平行四边形对边平行），

∴∠CDM＝∠AMD，∠DCM＝∠BMC，

∴∠ADM＝∠CDM，∠BCM＝∠DCM（两直线平行，内错角相等），

∵AD∥BC，

∴∠ADC＝∠BCD＝180°，

∴∠CDM+∠DCM＝ ∠ADC+ ∠BCD＝90°，

∴∠CMD＝90°，即∠CMD是直角．

故选：B．