题目内容
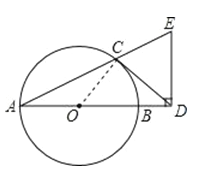
【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
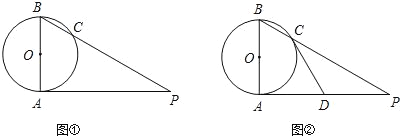
(1)如图①,若∠P=35°,求∠ABP的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
【答案】(1)55°;(2)证明见解析.
【解析】
(1)首先根据切线的性质判定∠BAP=90,然后利用直角三角形两锐角互余求出∠ABP;
(2)连接OC、OD、AC,证出∠OCD=90即可,由AB是直径,得到直角三角形ACP,根据直角三角形斜边上的中线等于斜边的一半得到CD=AD,从而△OAD≌△OCD,得到结论.
(1)解:∵AB是⊙O的直径,AP是⊙O的切线,
∴AB⊥AP,
∴∠BAP=90°;
又∵∠P=35°,
∴∠ABP=90°﹣35°=55°.
(2)证明:如图,连接OC,OD、AC.
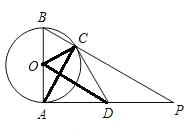
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),
∴∠ACP=90°;
又∵D为AP的中点,
∴AD=CD(直角三角形斜边上的中线等于斜边的一半);
在△OAD和△OCD中,
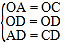 ,
,
∴△OAD≌△OCD(SSS),
∴∠OAD=∠OCD(全等三角形的对应角相等);
又∵AP是⊙O的切线,A是切点,
∴AB⊥AP,
∴∠OAD=90°,
∴∠OCD=90°,即直线CD是⊙O的切线.
故答案为:(1)55°;(2)证明见解析.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目