题目内容
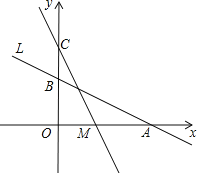
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,请直接写出此时t值和M点的坐标.
【答案】(1)A(4,0)、B(0,2);(2)0≤t≤4时,S△OCM=8﹣2t;t>4时,S△OCM=2t﹣8;(3)当t=2或6时,△COM≌△AOB,此时M(2,0)或(﹣2,0)
【解析】
(1)由直线L的函数解析式,令y=0求A点坐标,x=0求B点坐标;
(2)由面积公式S=![]() OMOC求出S与t之间的函数关系式;
OMOC求出S与t之间的函数关系式;
(3)若△COM≌△AOB,OM=OB,则t时间内移动了AM,可算出t值,并得到M点坐标.
(1)对于直线AB:y=﹣![]() x+2,
x+2,
当x=0时,y=2;当y=0时,x=4,
则A、B两点的坐标分别为A(4,0)、B(0,2);
(2)∵C(0,4),A(4,0)
∴OC=OA=4,
当0≤t≤4时,OM=OA﹣AM=4﹣t,S△OCM=![]() ×4×(4﹣t)=8﹣2t;
×4×(4﹣t)=8﹣2t;
当t>4时,OM=AM﹣OA=t﹣4,S△OCM=![]() ×4×(t﹣4)=2t﹣8;
×4×(t﹣4)=2t﹣8;
(3)∵OC=OA,∠AOB=∠COM=90°,
∴只需OB=OM,则△COM≌△AOB,
即OM=2,
此时,若M在x轴的正半轴时,t=2,
M在x轴的负半轴,则t=6.
故当t=2或6时,△COM≌△AOB,此时M(2,0)或(﹣2,0).

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案【题目】人寿保险公司的一张关于某地区的生命表的部分摘录如下:
年龄 | 活到该年龄的人数 | 在该年龄的死亡人数 |
40 | 80500 | 892 |
50 | 78009 | 951 |
60 | 69891 | 1200 |
70 | 45502 | 2119 |
80 | 16078 | 2001 |
… | … | … |
根据上表解下列各题:
(1)某人今年50岁,他当年去世的概率是多少?他活到80岁的概率是多少?
(保留三个有效数字)
(2)如果有20000个50岁的人参加人寿保险,当年死亡的人均赔偿金为10万元,预计保险公司需付赔偿的总额为多少?