题目内容
 如图在△ABC中,已知点D、E、F分别为边BC,AD,CE的中点,且△ABC的面积是4,则△BEF的面积是
如图在△ABC中,已知点D、E、F分别为边BC,AD,CE的中点,且△ABC的面积是4,则△BEF的面积是分析:依据三角形的面积公式及点D、E、F分别为边BC,AD,CE的中点,推出S△BEF=
S△ABC,从而求得△BEF的面积.
| 1 |
| 4 |
解答:解:∵点D、E、F分别为边BC,AD,CE的中点,
∴S△ABD=
S△ABC、S△BDE=
S△ABD、S△CDE=
S△ADC、S△BEF=
S△BEC,
∴S△BEF=
S△ABC;
∵△ABC的面积是4,
∴S△BEF=1.
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BEF=
| 1 |
| 4 |
∵△ABC的面积是4,
∴S△BEF=1.
点评:本题主要考查了三角形的面积公式:S=
底×高.
| 1 |
| 2 |

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 如图在△ABC中,已知∠B=45°,∠A=105°,AB=
如图在△ABC中,已知∠B=45°,∠A=105°,AB=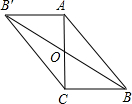 (2013•江西模拟)如图在ABC中,已知∠C=90°,AC=BC,BC=2,若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=( )
(2013•江西模拟)如图在ABC中,已知∠C=90°,AC=BC,BC=2,若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=( ) 完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C. .求BC的长.
.求BC的长.