题目内容
(2004•岳阳)如图在△ABC中,已知∠B=45°,∠A=105°,AB= .求BC的长.
.求BC的长.
【答案】分析:作AD⊥BC于D,构造了一个等腰直角三角形ABD和30度的直角三角形ACD,根据等腰直角三角形的性质可以求得AD=BD=1,再根据30度的直角三角形的性质求得CD的长即可.
解答: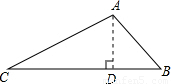 解:经过A点作AD⊥BC于D,
解:经过A点作AD⊥BC于D,
∵∠B=45°
∴∠BAD=45°
在Rt△ABD中,BD=AB•sin∠BAD=1
在Rt△ADC中,∠CAD=∠BAC-∠BAD=105°-45°=60°
∴tan∠CAD=
∴CD=AD•tan60°=1×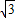 =
=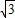
∴BC=CD+BD=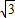 +1.
+1.
点评:此题只要作出BC边上的高,即可构造两个特殊的直角三角形,根据特殊角的锐角三角函数进行求解.
解答:
 解:经过A点作AD⊥BC于D,
解:经过A点作AD⊥BC于D,∵∠B=45°
∴∠BAD=45°
在Rt△ABD中,BD=AB•sin∠BAD=1
在Rt△ADC中,∠CAD=∠BAC-∠BAD=105°-45°=60°
∴tan∠CAD=

∴CD=AD•tan60°=1×
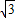 =
=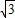
∴BC=CD+BD=
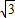 +1.
+1.点评:此题只要作出BC边上的高,即可构造两个特殊的直角三角形,根据特殊角的锐角三角函数进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
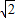 .求BC的长.
.求BC的长.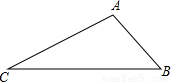
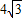 cm,半径r=4cm,则∠BAO= 度.
cm,半径r=4cm,则∠BAO= 度.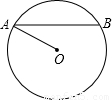
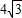 cm,半径r=4cm,则∠BAO= 度.
cm,半径r=4cm,则∠BAO= 度.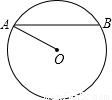
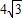 cm,半径r=4cm,则∠BAO= 度.
cm,半径r=4cm,则∠BAO= 度.