题目内容
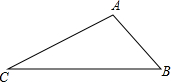如图在△ABC中，已知∠B=45°，∠A=105°，AB=| 2 |
分析：作AD⊥BC于D，构造了一个等腰直角三角形ABD和30度的直角三角形ACD，根据等腰直角三角形的性质可以求得AD=BD=1，再根据30度的直角三角形的性质求得CD的长即可．
解答：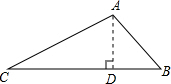
解：经过A点作AD⊥BC于D，
∵∠B=45°
∴∠BAD=45°
在Rt△ABD中，BD=AB•sin∠BAD=1
在Rt△ADC中，∠CAD=∠BAC-∠BAD=105°-45°=60°
∴tan∠CAD=
∴CD=AD•tan60°=1×
=
∴BC=CD+BD=
+1．
解：经过A点作AD⊥BC于D，∵∠B=45°
∴∠BAD=45°
在Rt△ABD中，BD=AB•sin∠BAD=1
在Rt△ADC中，∠CAD=∠BAC-∠BAD=105°-45°=60°
∴tan∠CAD=
| CD |
| AD |
∴CD=AD•tan60°=1×
| 3 |
| 3 |
∴BC=CD+BD=
| 3 |
点评：此题只要作出BC边上的高，即可构造两个特殊的直角三角形，根据特殊角的锐角三角函数进行求解．
练习册系列答案
阅读快车系列答案
相关题目
如图在△ABC中，已知点D、E、F分别为边BC，AD，CE的中点，且△ABC的面积是4，则△BEF的面积是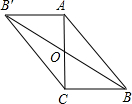
（2013•江西模拟）如图在ABC中，已知∠C=90°，AC=BC，BC=2，若以AC的中点O为旋转中心，将这个三角形旋转180°，点B落在点B′处，则BB′=（ ）
完成推理填空：如图在△ABC中，已知∠1+∠2=180°，∠3=∠B，试说明∠AED=∠C．
．求BC的长．