题目内容
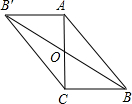（2013•江西模拟）如图在ABC中，已知∠C=90°，AC=BC，BC=2，若以AC的中点O为旋转中心，将这个三角形旋转180°，点B落在点B′处，则BB′=（ ）分析：由旋转的性质可知，OB=OB′，则BB′=2OB，又OC=OA=1，BC=2，在Rt△OBC中，由勾股定理求OB即可．
解答：解：∵△ABC绕AC的中点O旋转180°，
∴OB=OB′，则BB′=2OB，
又∵OC=OA=1，BC=2，
∴在Rt△OBC中，OB=
=
=
，
∴BB′=2OB=2
，
故选B．
∴OB=OB′，则BB′=2OB，
又∵OC=OA=1，BC=2，
∴在Rt△OBC中，OB=
| OC2+BC2 |
| 12+22 |
| 5 |
∴BB′=2OB=2
| 5 |
故选B．
点评：本题考查了旋转的性质，勾股定理的运用．关键是有旋转的性质得出BB′=2OB，再利用勾股定理求OB．
练习册系列答案
相关题目
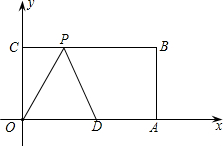（2013•江西模拟）如图，在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（10，0 ），C（0，4），点D是OA的中点，点P在BC边上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为（ ）
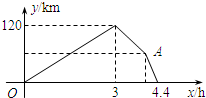车之间的距离y（km）与乙车行驶时间x（h）之间的函数图象．以下结论正确的是