题目内容
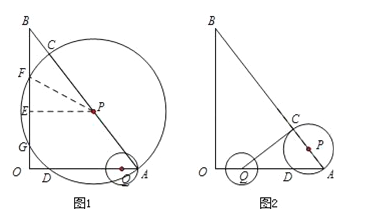
【题目】如图，在△AOB中，∠AOB为直角，OA=6，OB=8，半径为2的动圆圆心Q从点O出发，沿着OA方向以1个单位长度/秒的速度匀速运动，同时动点P从点A出发，沿着AB方向也以1个单位长度/秒的速度匀速运动，设运动时间为t秒（0＜t≤5）以P为圆心，PA长为半径的⊙P与AB、OA的另一个交点分别为C、D，连结CD、QC．
（1）当t为何值时，点Q与点D重合？
（2）当⊙Q经过点A时，求⊙P被OB截得的弦长．
（3）若⊙P与线段QC只有一个公共点，求t的取值范围．
【答案】（1）
；（2）
；（3）0＜t≤
或
＜t≤5．
【解析】试题分析：（1）由题意知CD⊥OA，所以△ACD∽△ABO，利用对应边的比求出AD的长度，若Q与D重合时，则，AD+OQ=OA，列出方程即可求出t的值；
（2）由于0＜t≤5，当Q经过A点时，OQ=4，此时用时为4s，过点P作PE⊥OB于点E，利用垂径定理即可求出⊙P被OB截得的弦长；
（3）若⊙P与线段QC只有一个公共点，分以下两种情况，①当QC与⊙P相切时，计算出此时的时间；②当Q与D重合时，计算出此时的时间；由以上两种情况即可得出t的取值范围．
试题解析：（1）∵OA=6，OB=8，∴由勾股定理可求得：AB=10，由题意知：OQ=AP=t，∴AC=2t，∵AC是⊙P的直径，∴∠CDA=90°，∴CD∥OB，∴△ACD∽△ABO，∴
，∴AD= 
，当Q与D重合时，AD+OQ=OA，∴
，∴t=
；
（2）当⊙Q经过A点时，如图1，OQ=OA﹣QA=4，∴t=
=4s，∴PA=4，∴BP=AB﹣PA=6，过点P作PE⊥OB于点E，⊙P与OB相交于点F、G，连接PF，∴PE∥OA，∴△PEB∽△AOB，∴
，∴PE=
，∴由勾股定理可求得：EF=
，由垂径定理可求知：FG=2EF=
；
（3）当QC与⊙P相切时，如图2，此时∠QCA=90°，∵OQ=AP=t，∴AQ=6﹣t，AC=2t，∵∠A=∠A，∠QCA=∠ABO，∴△AQC∽△ABO，∴
，∴
，∴t=
，∴当0＜t≤
时，⊙P与QC只有一个交点；
当QC⊥OA时，此时Q与D重合，由（1）可知：t=
，∴当
＜t≤5时，⊙P与QC只有一个交点，综上所述，当，⊙P与QC只有一个交点，t的取值范围为：0＜t≤
或
＜t≤5．
