题目内容
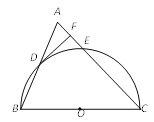
【题目】(9分)如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.
(1)判断DF与⊙O的位置关系,并证明你的结论;
(2)若BC=9,EF=1,求DF的长.
【答案】(1)DF与⊙O相切.证明见解析;(2)2![]() .
.
【解析】试题分析:(1)、连接OD,根据已知条件得出OD∥AC,从而得出切线;(2)、过点O作OG⊥EC,得出四边形OGFD为矩形,然后根据勾股定理求出OG的长度.
试题解析:(1)DF与⊙O相切.
连接OD. ∵AC=BC,OB=OD, ∴∠B=∠A ∠B=∠1 ∴∠A=∠1 ∴OD∥AC.
∵DF⊥AC ∴∠AFD=90° ∴∠ODF=∠AFD=90°
又∵OD是⊙O的半径 ∴DF与⊙O相切.
(2)过O作OG⊥EC交EC于点G.∵∠ODF=∠AFD=90° ∴四边形OGFD是矩形.
∴DF=OG,FG=OD=![]() BC=
BC=![]() ∵OG⊥EC, ∴CG=EG=FG-EF=
∵OG⊥EC, ∴CG=EG=FG-EF=![]() -1=
-1=![]() .
.
∴DF=OG=![]() =
=![]() =2
=2![]() .
.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目