题目内容
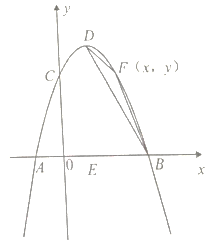
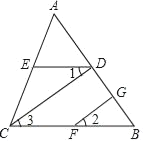
【题目】如图,在平面直角坐标系中,A(2,0),B ( 2,0),C为 y 轴负半轴上一点,D是第四象限内一动点,且始终有BDA 2ACO 成立,过C 点作CE BD 于点 E .
(1)求证:DAC DBC ;
(2)若点 F 在 AD 的延长线上,求证:CD 平分BDF ;

【答案】(1)见解析;(2)见解析.
【解析】
(1)根据轴对称的性质可知△ABC是等腰三角形,由三线合一可得∠ACB=2∠ACO,从而∠ACB=BDA,然后利用三角形的内角和即可得到结论;
(2)过C作CN⊥AF于N,根据AAS证明△BCE≌△ACN,可证CE=CN,然后根据角平分线的判定方法可得结论.
证明:(1)∵A(2,0),B ( 2,0),
∴OA=OB,
∴∠ACO=∠BCO,
∴ACB 2ACO,
∵BDA 2ACO,
∴∠ACB=BDA,
∵∠DAC =180°-∠BDA-∠AGD,
∴∠DBC =180°-∠ACB-∠BGC,
∴DAC DBC ;
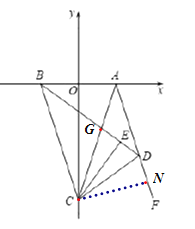
(2)过C作CN⊥AF于N,
∴∠BEC=∠CED=∠CND=90°;
在△BCE与△ACN中,
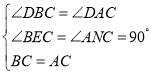 ,
,
∴△BCE≌△ACN,
∴CE=CN,
∴CD是∠BDF的角平分线;

【题目】随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展,某旅游公司对我市一企业个人旅游年消费情况进行问卷调查,随机抽查部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成尚不完整的表和图(如图).
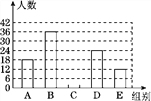
组别 | 个人年消费金额x/元 | 频数(人数) | 频率 |
A | x≤2 000 | 18 | 0.15 |
B | 2 000<x≤4 000 | a | b |
C | 4 000<x≤6 000 | ||
D | 6 000<x≤8 000 | 24 | 0.20 |
E | x>8 000 | 12 | 0.10 |
合计 | c | 1.00 |
根据以上信息回答下列问题:
(1)a=________,b=________,c=________,并将条形统计图补充完整;
(2)在这次调查中,个人年消费金额的中位数出现在________组;
(3)若这个企业有3 000名员工,请你估计个人旅游年消费金额在6 000元以上的人数.